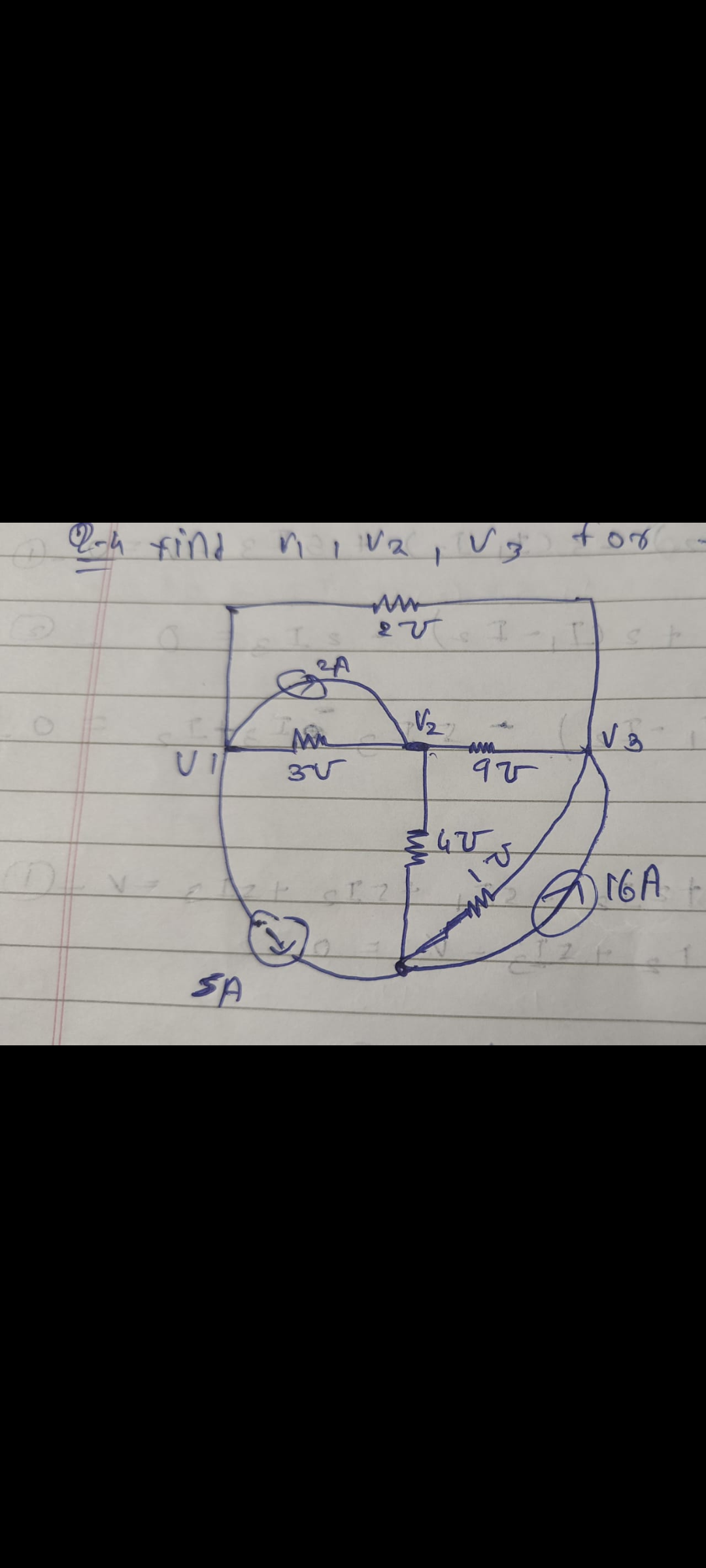
Find I1, V2, and V3 in the given circuit.

Steps to Solve

1. Identify the currents and voltages
   From the circuit diagram, let’s assign the currents:

• ( I_1 ) is the current through the left branch.
• ( I_2 ) is the current through the upper right branch.
• ( I_3 = 2A ) is given as flowing downwards in the lower branch.

2. Apply Kirchhoff's Current Law (KCL)
   At the junction where the currents meet:
   $$ I_1 + I_2 - I_3 = 0 $$
   Substituting ( I_3 ):
   $$ I_1 + I_2 - 2 = 0 $$
   This simplifies to:
   $$ I_1 + I_2 = 2 \quad (1) $$

3. Set up Kirchhoff's Voltage Law (KVL) for loop analysis
   For the loop on the left side containing ( V_1 ) and resistors:
   $$ - V_1 + 3 + 2I_1 + 2 = 0 $$
   Thus,
   $$ V_1 + 2I_1 = 5 \quad (2) $$

4. Analyze the upper right loop in a similar fashion
   For the upper loop with ( V_2 ) and resistors:
   $$ -V_2 + 9 - 4I_2 + 3 = 0 $$
   Thus,
   $$ V_2 - 4I_2 + 12 = 0 $$ and rearranging gives
   $$ V_2 = 4I_2 - 12 \quad (3) $$

5. Set up the equations from the voltage laws
   Now analyze the lower loop that connects with ( V_3 ):
   $$ -4 - V_3 + 9 + 16 = 0 $$
   This gives us:
   $$ V_3 = 9 - 4 - 16 = -11 \quad (4) $$

6. Substituting to find values
   From equation (1):
   $$ I_1 + I_2 = 2 $$

Using equation (3):
We can find ( I_2 ) by eliminating variables: substituting ( I_2 = 2 - I_1 ) into equation (3). Thus:
$$ V_2 = 4(2 - I_1) - 12 $$
Expanding gives us:
$$ V_2 = 8 - 4I_1 - 12 $$
Simplifying gives:
$$ V_2 = -4I_1 - 4 $$
This gives us a relationship which can be substituted back to find individual unknowns.

7. Solving for ( I_1 ) and ( I_2 )
   Using previous equations interactively should yield the values needed.