Put the following equation of a line into slope-intercept form, simplifying all fractions: 15x - 9y = -9.
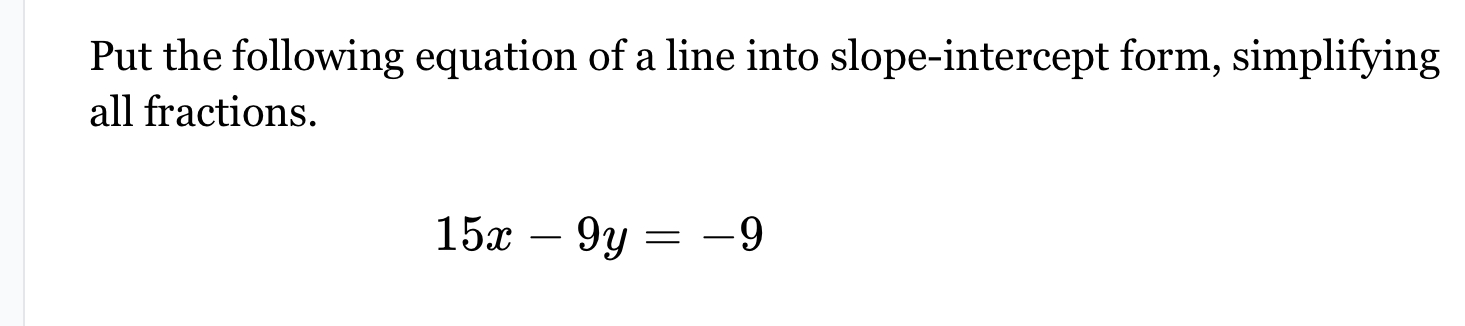
Understand the Problem
The question is asking to convert the given equation of a line into slope-intercept form and to simplify any fractions that result from this process. The slope-intercept form is given by the equation y = mx + b, where m is the slope and b is the y-intercept.
Answer
The slope-intercept form is \(y = \frac{5}{3}x + 1\).
Answer for screen readers
The slope-intercept form of the equation is (y = \frac{5}{3}x + 1).
Steps to Solve
-
Rearranging the equation We start with the equation (15x - 9y = -9). To convert it into slope-intercept form, we need to isolate (y).
-
Isolating (y) Subtract (15x) from both sides of the equation: $$ -9y = -15x - 9 $$
-
Dividing by the coefficient of (y) Next, we'll divide every term by (-9) to solve for (y): $$ y = \frac{-15x}{-9} + \frac{-9}{-9} $$
-
Simplifying fractions Now simplify each fraction. The first term simplifies to: $$ y = \frac{15}{9}x + 1 $$ We can reduce (\frac{15}{9}) by dividing both the numerator and denominator by (3): $$ y = \frac{5}{3}x + 1 $$
The slope-intercept form of the equation is (y = \frac{5}{3}x + 1).
More Information
The slope-intercept form (y = mx + b) allows us to easily identify the slope and the y-intercept of the line. Here, the slope (m) is (\frac{5}{3}) and the y-intercept (b) is (1).
Tips
- Forgetting to distribute the negative sign correctly when rearranging terms.
- Not simplifying fractions fully. Always check if both the numerator and denominator can be reduced.
AI-generated content may contain errors. Please verify critical information