Factor the expression completely: x^2y + x^4y.
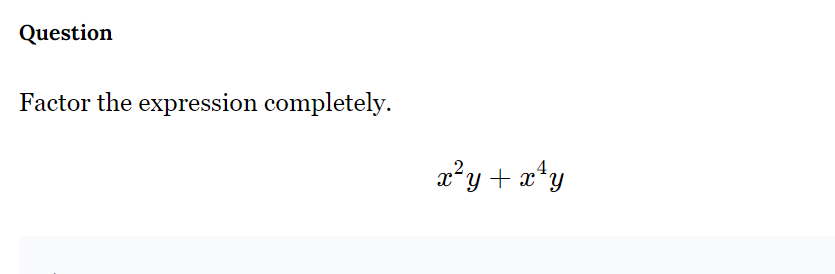
Understand the Problem
The question is asking to factor the given algebraic expression completely. This involves identifying the common factors in each term of the expression.
Answer
The factored expression is: $x^{2}y(1 + x^{2})$.
Answer for screen readers
The factored expression is:
$$ x^{2}y(1 + x^{2}) $$
Steps to Solve
-
Identify common factors
Look at the expression $x^{2}y + x^{4}y$. The common factors in both terms are $y$ and $x^{2}$. -
Factor out the common factors
Factor out the common factors from the expression:
$$ y \cdot x^{2} (1 + x^{2}) $$ -
Rewrite the expression
Now the expression can be rewritten as:
$$ x^{2}y(1 + x^{2}) $$
The factored expression is:
$$ x^{2}y(1 + x^{2}) $$
More Information
Factoring is a fundamental skill in algebra that allows expressions to be simplified and made easier to work with. The expression $x^{2}y(1 + x^{2})$ can be useful in further mathematical operations, such as solving equations or evaluating functions.
Tips
- Forgetting to factor out all common elements, which can lead to incomplete factorizations. Always double-check that all common factors have been included.
AI-generated content may contain errors. Please verify critical information