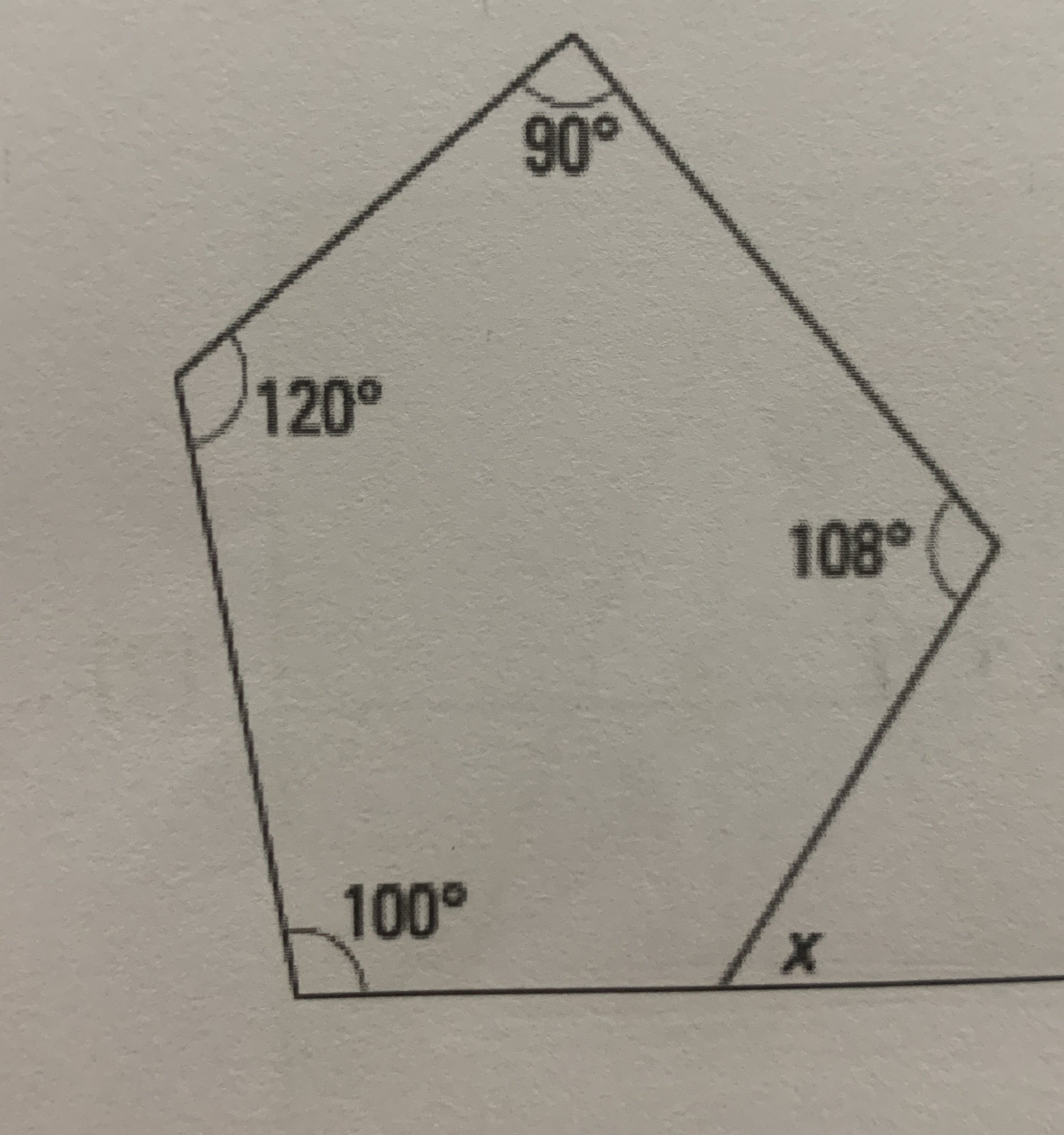
What is the value of x in the given polygon with angles 90°, 120°, 100°, and 108°?
Understand the Problem
The question involves finding the value of an unknown angle, x, in a polygon with given angles. We need to apply the properties of the sum of interior angles of a polygon to solve for x.
Answer
The unknown angle \( x \) is \( 122^\circ \).
Answer for screen readers
The value of angle ( x ) is ( 122^\circ ).
Steps to Solve
- Determine the number of sides of the polygon
The polygon shown has five angles, which means it is a pentagon.
- Calculate the sum of interior angles
The formula for the sum of the interior angles of a polygon is given by:
$$ \text{Sum of interior angles} = (n - 2) \times 180^\circ $$
where ( n ) is the number of sides. For a pentagon, ( n = 5 ):
$$ \text{Sum of interior angles} = (5 - 2) \times 180^\circ = 3 \times 180^\circ = 540^\circ $$
- Set up the equation with known angles
The known angles in the pentagon are ( 90^\circ ), ( 120^\circ ), ( 100^\circ ), and ( 108^\circ ). We can express the sum of all angles including the unknown angle ( x ):
$$ 90^\circ + 120^\circ + 100^\circ + 108^\circ + x = 540^\circ $$
- Combine known angles
Add the known angles together:
$$ 90^\circ + 120^\circ + 100^\circ + 108^\circ = 418^\circ $$
- Solve for ( x )
Now substitute back into the equation:
$$ 418^\circ + x = 540^\circ $$
To find ( x ), subtract ( 418^\circ ) from both sides:
$$ x = 540^\circ - 418^\circ $$
- Calculate the value of ( x )
Perform the subtraction:
$$ x = 122^\circ $$
The value of angle ( x ) is ( 122^\circ ).
More Information
The sum of the interior angles in a pentagon is always ( 540^\circ ). This property is useful for solving problems involving polygons and their angles.
Tips
- Forgetting to use the correct formula for the sum of interior angles.
- Adding the angles incorrectly. Double-check the arithmetic to avoid errors.
AI-generated content may contain errors. Please verify critical information