A circle passes through the origin whose centre lies on αx² + y² - Hx - 6y + 10 = 0 and it cuts the curve orthogonally.
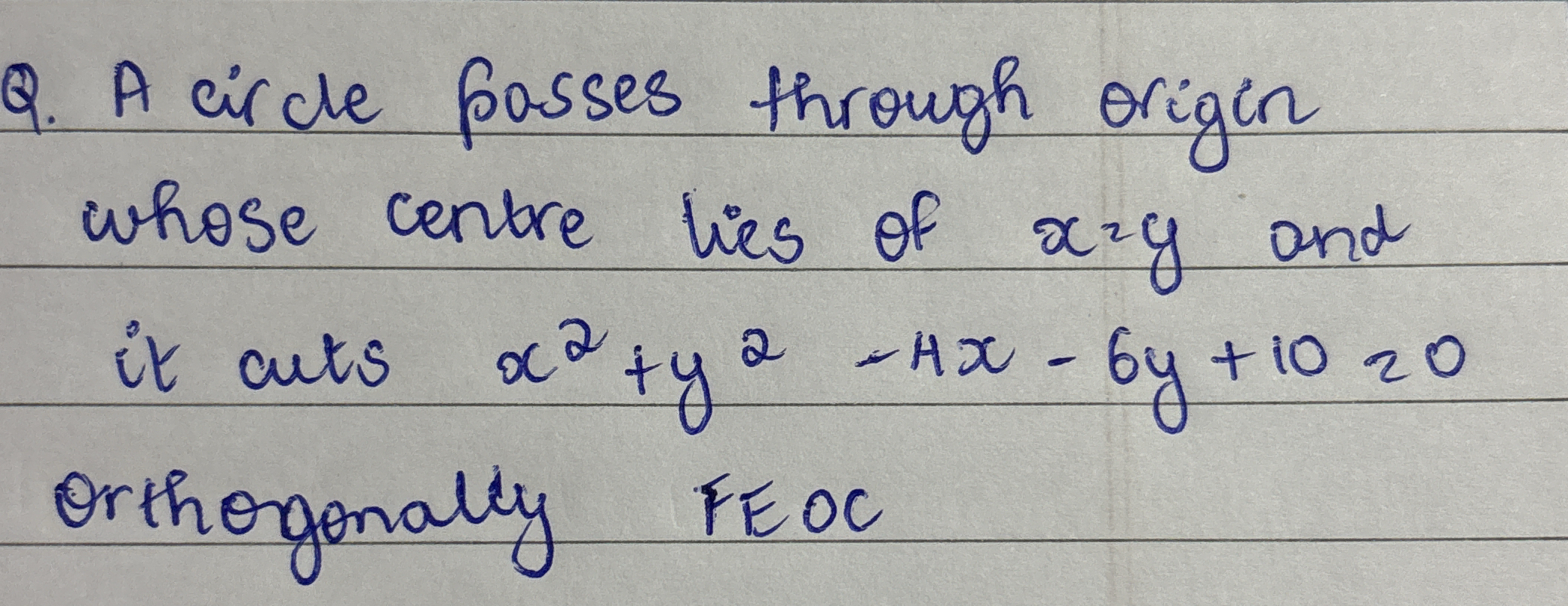
Understand the Problem
The question is asking to find the equation of a circle that passes through the origin and whose center lies on the line represented by the equation αx² + y² - Hx - 6y + 10 = 0. The circle also intersects another given curve orthogonally. The task likely involves deriving mathematical relationships and equations to solve for the unknowns involved.
Answer
The equation of the circle is $(x - h)^2 + (y - k)^2 = h^2 + k^2$ where $h$ and $k$ satisfy the curve equation and orthogonality condition.
Answer for screen readers
The equation of the circle that meets the conditions is given by: $$ (x - h)^2 + (y - k)^2 = h^2 + k^2 $$ where $h$ and $k$ satisfy $\alpha h^2 + k^2 - Hh - 6k + 10 = 0$ and the orthogonality condition.
Steps to Solve
- Identify the center of the circle
Let the center of the circle be $(h, k)$. Since the circle passes through the origin, we can express the radius $r$ in terms of $h$ and $k$ as follows: $$ r = \sqrt{h^2 + k^2} $$
- Equation of the circle
The equation of the circle can be written as: $$ (x - h)^2 + (y - k)^2 = r^2 $$ Substituting for $r$, we have: $$ (x - h)^2 + (y - k)^2 = h^2 + k^2 $$
- Substituting the center's constraint
Since the center $(h, k)$ lies on the curve given by the equation $\alpha x^2 + y^2 - Hx - 6y + 10 = 0$, we can substitute $(h, k)$ into this equation: $$ \alpha h^2 + k^2 - Hh - 6k + 10 = 0 $$
- Orthogonality condition
For the circle to intersect orthogonally with the curve, the following relationship must hold: $$ 2(x_1 - h)(x_2 - h) + 2(y_1 - k)(y_2 - k) = r^2 $$ We need to work with this condition to find values of $h$ and $k$ that satisfy both the circle’s and the curve’s equations.
- Simplifying the equations
Expand and simplify the equations derived from the circle and orthogonality condition:
- From the equation of the circle: $$ x^2 - 2hx + y^2 - 2ky + (h^2 + k^2 - r^2) = 0 $$
- Using the orthogonality condition, you can substitute various points $(x_1, y_1)$ and $(x_2, y_2)$ based on the curve's equation and relate them back to $(h, k)$.
- Solving the system
Solve the system of equations involving $(h, k)$ both from the curve equation and the orthogonality condition to find specific values for $\alpha, H, k$.
The equation of the circle that meets the conditions is given by: $$ (x - h)^2 + (y - k)^2 = h^2 + k^2 $$ where $h$ and $k$ satisfy $\alpha h^2 + k^2 - Hh - 6k + 10 = 0$ and the orthogonality condition.
More Information
This solution involves finding the relationship between the circle and a curve through geometric and algebraic methods. The orthogonality condition indicates that the tangents at the points of intersection create a right angle.
Tips
- Misapplying the orthogonality condition by not correctly identifying points of intersection.
- Incorrectly substituting values into the circle or curve equations.
- Ignoring the implications of passing through the origin when deriving radius or center.
AI-generated content may contain errors. Please verify critical information