Evaluate the integral ∫ (3√(1 + 4√x) / √x) dx.
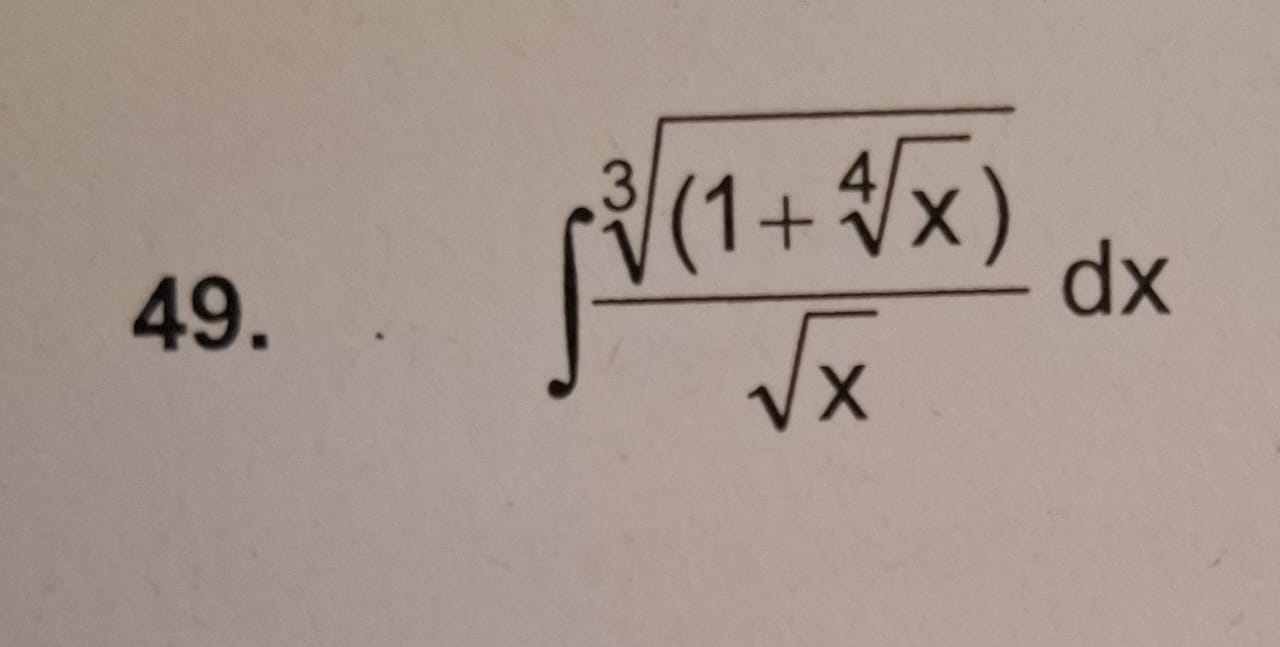
Understand the Problem
The question is asking to evaluate a definite integral involving square root functions. The integral to be solved is from the expression provided in the image.
Answer
$$ I = (1 + 4\sqrt{x})^{3/2} + C $$
Answer for screen readers
The final result of the integral is
$$ I = (1 + 4\sqrt{x})^{3/2} + C $$
Steps to Solve
- Rewrite the Integral
The integral to be solved is
$$ I = \int \frac{3\sqrt{1 + 4\sqrt{x}}}{\sqrt{x}} , dx $$
To simplify the expression, we can make the substitution $ u = \sqrt{x}$. Thus, $ x = u^2 $ and $ dx = 2u , du $.
- Substitute and Simplify
After substitution, we have:
$$ I = \int \frac{3\sqrt{1 + 4u}}{u} \cdot 2u , du = 6\int \sqrt{1 + 4u} , du $$
- Evaluate the Integral
We can simplify further by using the substitution $ v = 1 + 4u$, which gives $ du = \frac{1}{4} dv $.
Now the limits change:
When $ u = 0 \rightarrow v = 1 $, and as $ u \rightarrow \infty$, $ v \rightarrow \infty $.
The integral becomes:
$$ I = 6 \cdot \frac{1}{4} \int \sqrt{v} , dv = \frac{3}{2} \int v^{1/2} , dv $$
- Integral of ( v^{1/2} )
The integral of ( v^{1/2} ) is:
$$ \int v^{1/2} , dv = \frac{2}{3} v^{3/2} + C $$
Substituting back, we have:
$$ I = \frac{3}{2} \cdot \frac{2}{3} v^{3/2} + C = v^{3/2} + C $$
- Back Substitute for ( u ) and ( x )
Re-substituting for ( v ):
$$ v = 1 + 4u $$ $$ u = \sqrt{x} $$
Thus,
$$ I = (1 + 4\sqrt{x})^{3/2} + C $$
The final result of the integral is
$$ I = (1 + 4\sqrt{x})^{3/2} + C $$
More Information
This integral involves multi-variable substitutions and highlights the relationship between different functions through algebraic manipulation. The use of trigonometric or polynomial substitutions can vastly simplify the computation process.
Tips
- Forgetting to change the limits correctly when substituting variables.
- Neglecting to simplify the integral before solving.
- Errors during the integration process after substitution.
AI-generated content may contain errors. Please verify critical information