Evaluate each expression below: a. √64 b. √32 c. √27 d. √10000
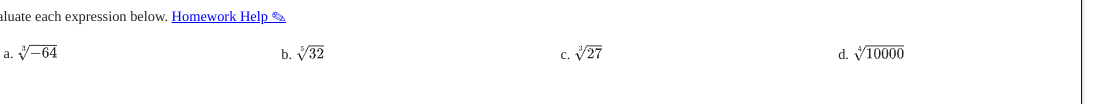
Understand the Problem
The question is asking to evaluate four different square root expressions: √64, √32, √27, and √10000.
Answer
a. $8$, b. $4\sqrt{2}$, c. $3\sqrt{3}$, d. $100$
Answer for screen readers
a. $8$
b. $4\sqrt{2}$
c. $3\sqrt{3}$
d. $100$
Steps to Solve
- Evaluate $\sqrt{64}$
The square root of 64 can be calculated by finding the number that, when multiplied by itself, gives 64.
$$\sqrt{64} = 8$$
- Evaluate $\sqrt{32}$
To evaluate $\sqrt{32}$, we can simplify it first. We know that $32$ can be expressed as $16 \times 2$, where $16$ is a perfect square.
Using this, we get:
$$\sqrt{32} = \sqrt{16 \times 2} = \sqrt{16} \times \sqrt{2} = 4\sqrt{2}$$
- Evaluate $\sqrt{27}$
Similarly, for $\sqrt{27}$, we can factor it into perfect squares:
$$\sqrt{27} = \sqrt{9 \times 3} = \sqrt{9} \times \sqrt{3} = 3\sqrt{3}$$
- Evaluate $\sqrt{10000}$
Lastly, to find $\sqrt{10000}$, we find the number that, when squared, produces 10000.
$$\sqrt{10000} = 100$$
a. $8$
b. $4\sqrt{2}$
c. $3\sqrt{3}$
d. $100$
More Information
Square roots help determine the principal value of a number that, when squared, results in the given value. In this case, perfect squares were used to simplify certain expressions.
Tips
- Forgetting to simplify square roots such as $\sqrt{32}$ and $\sqrt{27}$.
- Confusing the values when estimating square roots without calculation.
AI-generated content may contain errors. Please verify critical information