Evaluate ∬_D (x + 2y) dA, where D is the region bounded by the parabolas y = 2x² and y = 1 + x².
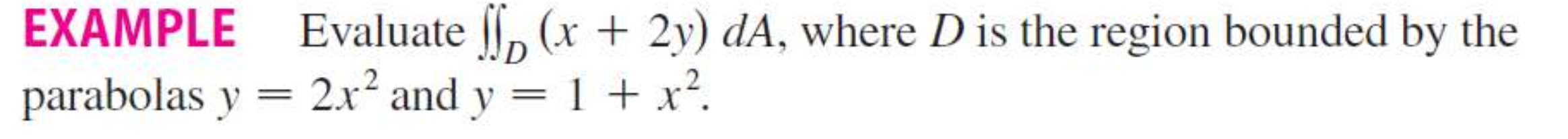
Understand the Problem
The question is asking us to evaluate a double integral over a region defined by two parabolas. We're expected to set up and calculate the integral of the expression (x + 2y) over the specified region D, which is enclosed by the parabolas y = 2x² and y = 1 + x².
Answer
The value of the double integral is \( \frac{32}{15} \).
Answer for screen readers
The value of the double integral is ( \frac{32}{15} ).
Steps to Solve
- Find Points of Intersection
To determine the area ( D ) bounded by the parabolas, we need to find the points where the equations intersect:
Set ( 2x^2 = 1 + x^2 ).
This simplifies to: $$ 2x^2 - x^2 - 1 = 0 \Rightarrow x^2 - 1 = 0 $$ Thus, ( x = \pm 1 ).
- Set up the Limits for the Integral
The region ( D ) is vertically bounded by the parabolas from ( x = -1 ) to ( x = 1 ). The upper curve is ( y = 1 + x^2 ) and the lower curve is ( y = 2x^2 ).
We can set up the double integral as follows: $$ \int_{-1}^{1} \int_{2x^2}^{1+x^2} (x + 2y) , dy , dx $$
- Evaluate the Inner Integral
Evaluate the inner integral: $$ \int_{2x^2}^{1+x^2} (x + 2y) , dy $$ The integral of ( (x + 2y) ) with respect to ( y ) is: $$ xy + y^2 $$ Calculating the bounds: $$ \left[ x(1+x^2) + (1+x^2)^2 \right] - \left[ x(2x^2) + (2x^2)^2 \right] $$
Calculating it requires simplifying:
- Upper bound: $$ x(1+x^2) + (1+x^2)^2 = x + x^3 + 1 + 2x^2 + x^4 $$
- Lower bound: $$ x(2x^2) + (2x^2)^2 = 2x^3 + 4x^4 $$
Thus, the difference is: $$ x + x^3 + 1 + 2x^2 + x^4 - (2x^3 + 4x^4) = x + 1 + 2x^2 - x^3 - 3x^4 $$
- Evaluate the Outer Integral
Now, we need to integrate: $$ \int_{-1}^{1} (x + 1 + 2x^2 - x^3 - 3x^4) , dx $$ Break it into individual integrals: $$ \int_{-1}^{1} x , dx + \int_{-1}^{1} 1 , dx + 2\int_{-1}^{1} x^2 , dx - \int_{-1}^{1} x^3 , dx - 3\int_{-1}^{1} x^4 , dx $$
Using symmetry:
- The integrals of odd functions ( \int_{-1}^{1} x , dx ) and ( \int_{-1}^{1} x^3 , dx ) are zero.
- The integrals of even functions ( \int_{-1}^{1} x^2 , dx = \frac{2}{3} ) and ( \int_{-1}^{1} x^4 , dx = \frac{2}{5} ).
Thus, we have: $$ 0 + 2 + 2(\frac{2}{3}) - 0 - 3(\frac{2}{5}) = 2 + \frac{4}{3} - \frac{6}{5} $$
Finding a common denominator (15): $$ 2 = \frac{30}{15}, \quad \frac{4}{3} = \frac{20}{15}, \quad \frac{6}{5} = \frac{18}{15} $$ So, $$ \frac{30 + 20 - 18}{15} = \frac{32}{15} $$
- Final Answer
Thus, the value of the integral is: $$ \frac{32}{15} $$
The value of the double integral is ( \frac{32}{15} ).
More Information
This integral represents the "volume" under the surface defined by the function ( x + 2y ) within the region bounded by the two parabolas. Evaluating double integrals like this one is common in multivariable calculus, especially for calculating areas and volumes.
Tips
- Skipping the intersection points: Failing to determine where the curves intersect can lead to incorrect limits of integration.
- Not simplifying correctly: When calculating the integrals, ensure to simplify expressions carefully to avoid mistakes.
AI-generated content may contain errors. Please verify critical information