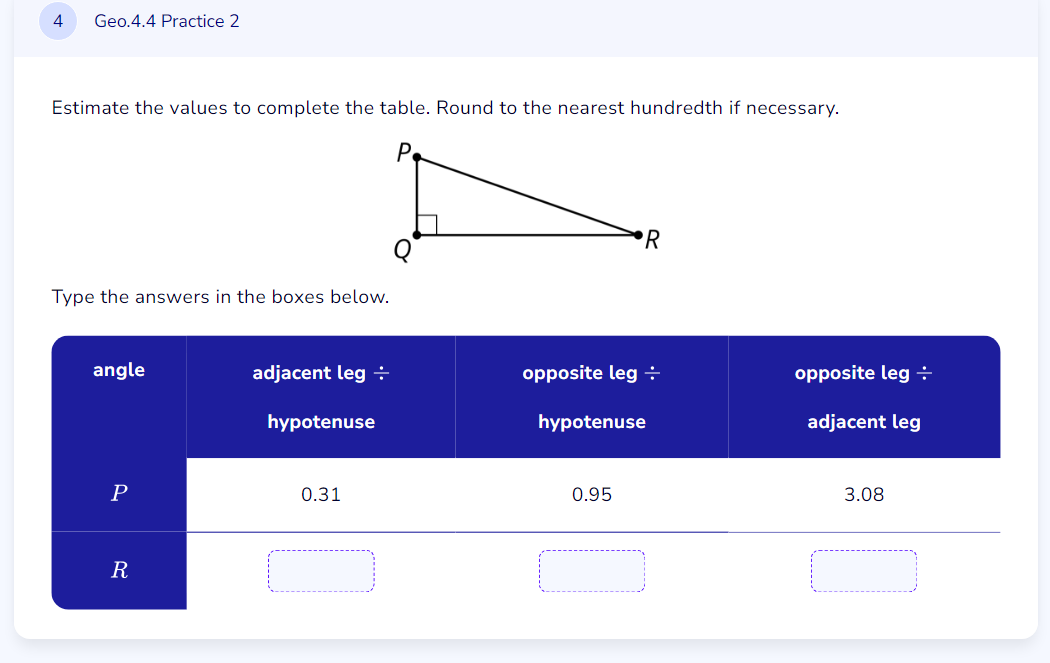
Estimate the values to complete the table. Round to the nearest hundredth if necessary.

Steps to Solve

1. Calculate the trigonometric ratios for angle P

We have the adjacent leg divided by the hypotenuse (0.31) and the opposite leg divided by the hypotenuse (0.95).

For angle P, we can use the cosine and sine definitions:

• $\cos(P) = \frac{\text{adjacent leg}}{\text{hypotenuse}}$
• $\sin(P) = \frac{\text{opposite leg}}{\text{hypotenuse}}$

Using these ratios:

• Hypotenuse = 1 (assuming it as 1 unit for simplicity)

From the given values:

• The adjacent leg can be calculated as $0.31 \cdot \text{Hypotenuse} = 0.31 \cdot 1 = 0.31$
• The opposite leg can be calculated as $0.95 \cdot \text{Hypotenuse} = 0.95 \cdot 1 = 0.95$

Next, we must determine angle R.

2. Determine the trigonometric ratios for angle R

The triangle’s angle P and angle R are complementary, since the sum of angles in a right triangle is (90^\circ). Therefore:

$$ R = 90^\circ - P $$

Now we can write the trigonometric ratios for angle R:

• For adjacent leg divided by hypotenuse: $\cos(R) = \frac{\text{opposite leg}}{\text{hypotenuse}} = \frac{0.95}{1} = 0.95$
• For opposite leg divided by hypotenuse: $\sin(R) = \frac{\text{adjacent leg}}{\text{hypotenuse}} = \frac{0.31}{1} = 0.31$

3. Calculate opposite leg divided by adjacent leg

To complete the opposite leg divided by adjacent leg ratio for angle R:

$$ \frac{\text{opposite leg}}{\text{adjacent leg}} = \frac{0.95}{0.31} $$

Calculating this gives approximately:

$$ \frac{0.95}{0.31} \approx 3.06 $$

4. Final values for the table

Now we can summarize the values:

• For angle P:

  • Adjacent leg $\div$ Hypotenuse = 0.31
  • Opposite leg $\div$ Hypotenuse = 0.95

• For angle R:

  • Adjacent leg $\div$ Hypotenuse = 0.95
  • Opposite leg $\div$ Hypotenuse = 0.31
  • Opposite leg $\div$ Adjacent leg $\approx 3.06$