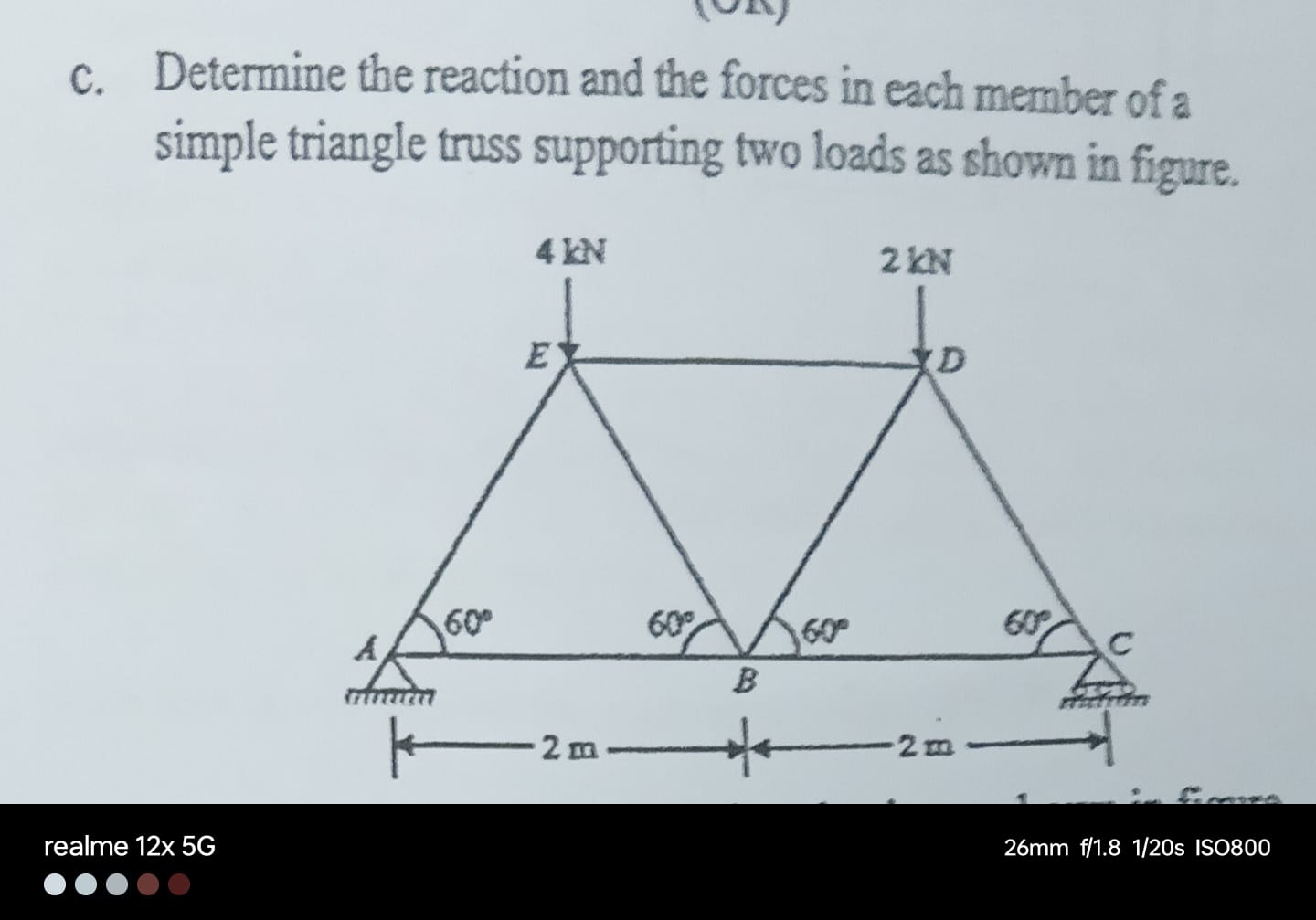
Determine the reaction and the forces in each member of a simple triangle truss supporting two loads as shown in figure.

Steps to Solve

1. Identify Supports and External Loads

Determine the supports at points A and B. Point A is a pin support, allowing rotation but resisting vertical and horizontal forces. B is a roller support, allowing vertical movement but resisting vertical forces. The external loads are 4 kN at point E and 2 kN at point D.

2. Calculate Reaction Forces

Using equilibrium equations, set up the following:

• Sum of vertical forces ($\Sigma F_y = 0$): $$ R_A + R_B - 4 , \text{kN} - 2 , \text{kN} = 0 $$

• Sum of horizontal forces ($\Sigma F_x = 0$): $$ R_{Ax} = 0 $$ (since there are no horizontal loads)

• Taking moments around point A to find $R_B$ (clockwise moments are positive): $$ \Sigma M_A = 0 = R_B \cdot 4 - 4 \cdot 2 - 2 \cdot 2 $$ Solve for $R_B$.

3. Calculate the Reaction at A

From the equation for vertical forces, substitute the value of $R_B$ back to find $R_A$.

4. Analyze Each Member of the Truss

Use the method of joints to analyze forces in the truss members.

For joint E:

• From equilibrium, sum forces in the x and y directions.
• For joint D, perform a similar analysis.

5. Use Trigonometric Relationships for Angles

For any non-vertical members, resolve the forces into horizontal and vertical components using the $60^\circ$ angles:

• For any member, if $F$ is the force in the member: $$ F_x = F \cdot \cos(60^\circ) $$ $$ F_y = F \cdot \sin(60^\circ) $$

6. Solve for the Member Forces

Set up equations for each joint and solve for the unknown forces in members AE, ED, DB, and BC.