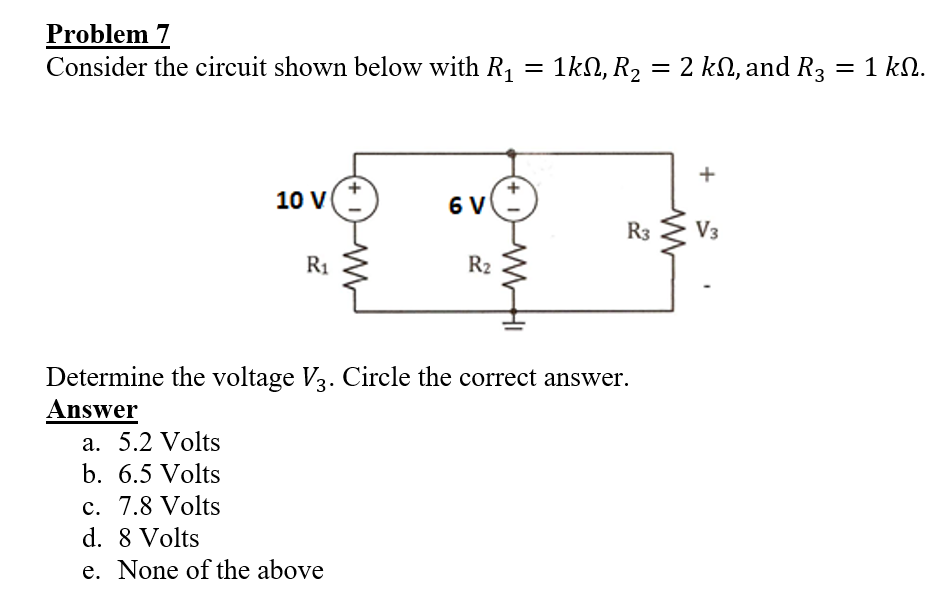
Determine the voltage V3. Circle the correct answer.
Understand the Problem
The question is asking to calculate the voltage V3 in a given electrical circuit with specified resistor values and voltage sources. To solve this, we will analyze the circuit and apply relevant circuit analysis techniques such as Kirchhoff's laws or voltage divider rules.
Answer
$3.33\,V$
Answer for screen readers
The final answer is: $$ V3 \approx 3.33,V $$
Steps to Solve
-
Identify Total Voltage and Resistance
The total voltage from the source is the sum of the voltage sources: $$ V_{total} = 10,V - 6,V = 4,V $$
-
Calculate Total Resistance
The resistors $R1$ and $R2$ are in series. Thus, the total resistance $R_{total1}$ is: $$ R_{total1} = R1 + R2 = 1,k\Omega + 2,k\Omega = 3,k\Omega $$
-
Voltage across R2
Using the voltage divider rule, the voltage across $R2$ can be found by: $$ V_{R2} = V_{total} \cdot \frac{R2}{R_{total1}} $$ $$ V_{R2} = 4,V \cdot \frac{2,k\Omega}{3,k\Omega} $$ $$ V_{R2} = \frac{8}{3},V \approx 2.67,V $$
-
Calculate Voltage V3
The voltage $V3$ across $R3$ can be calculated using: $$ V3 = 6,V - V_{R2} $$ $$ V3 = 6,V - 2.67,V $$ $$ V3 \approx 3.33,V $$
-
Verify Calculated Voltage
Re-check the polarities and connections in the circuit to ensure that the calculated voltage matches the voltage polarity according to Kirchhoff's Voltage Law.
The final answer is: $$ V3 \approx 3.33,V $$
More Information
The calculated voltage $V3$ indicates the potential drop across the resistor $R3$ as influenced by the supplied voltages from the sources and the resistive components present in the circuit.
Tips
- Failing to correctly apply the voltage divider rule can lead to inaccurate voltage calculations across individual resistors.
- Neglecting the effects of polarity when combining voltage sources can result in miscalculating the total voltage.
AI-generated content may contain errors. Please verify critical information