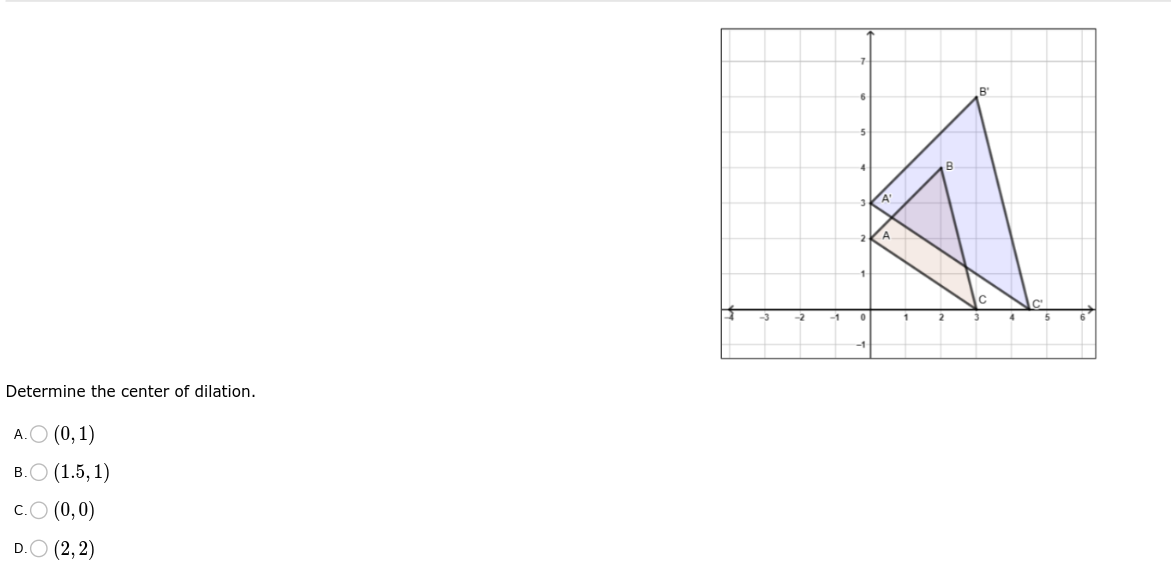
Determine the center of dilation.

Steps to Solve

1. Identify the Coordinates of Points Identify the coordinates of the points for both the original and dilated figures. The original triangle has vertices:

   • ( A(2, 2) )
   • ( B(3, 3) )
   • ( C(1, 1) )

   The dilated triangle has vertices:

   • ( A'(1, 1) )
   • ( B'(2, 2) )
   • ( C'(0.5, 0.5) )

2. Determine the Relationships Between Points To find the center of dilation, we need to observe the ratio of the distances from the center to the original points and the corresponding dilated points. Set the center of dilation as ( O(x, y) ).

3. Use the Dilation Formula The dilation formula relates the original point ( P ) and the dilated point ( P' ): $$ P' = O + k(P - O) $$ Where ( O ) is the center of dilation, ( k ) is the scale factor, and ( P ) and ( P' ) are original and image points, respectively.

4. Solve for Each Pair of Points Taking two pairs of corresponding points, plug in the coordinates:

   • For point ( A(2, 2) ) and ( A'(1, 1) ): $$ 1 = x + k(2 - x) $$ $$ 1 = y + k(2 - y) $$

   • For point ( B(3, 3) ) and ( B'(2, 2) ): $$ 2 = x + k(3 - x) $$ $$ 2 = y + k(3 - y) $$

5. Set Up and Solve System of Equations You will have a system of equations that you can solve for ( x ) and ( y ). Finding ( k ) can help determine the right coordinates.

6. Evaluate Potential Centers Based on solutions to the equations, plug in options A, B, C, and D to check which point satisfies the conditions derived above.