In how many ways can 6 boys and 2 girls be seated in a row if 2 girls must seat together? Expand (1 + x)^1/2 up to the term containing x^3 and use it to approximate √10.
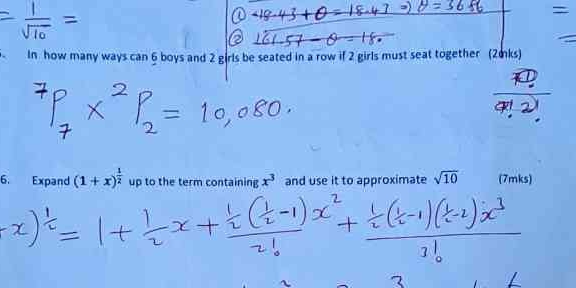
Understand the Problem
The question involves solving a combinatorial problem about seating arrangements and approximating a mathematical expression using a series expansion. It asks for the number of ways to arrange boys and girls under certain conditions and involves expanding a function to approximate the square root.
Answer
Seating arrangements: $10,080$; Approximate $\sqrt{10} \approx 3.16$.
Answer for screen readers
The total number of ways the boys and girls can be seated is $10,080$.
The approximation for $\sqrt{10}$, using the series expansion, is approximately $3.16$ (after calculating each term).
Steps to Solve
-
Arrange Boys Together with Girls Since 2 girls must sit together, consider them as a single unit or block.
- This means we now have 6 boys + 1 girl block = 7 units to arrange.
- The number of ways to arrange these 7 units is given by $7!$.
-
Arrange Girls Inside Their Block Now, within the girl block, the 2 girls can be arranged among themselves.
- The number of ways to arrange 2 girls is $2!$.
-
Calculate Total Arrangements Multiply the two results obtained above to find the total number of arrangements:
$$ \text{Total Arrangements} = 7! \times 2! $$
- Calculate $7! = 5040$ and $2! = 2$.
- Thus, total arrangements = $5040 \times 2 = 10080$.
-
Expand the Series For the second part, we need to approximate $\sqrt{10}$ by expanding $(1 + x)^{\frac{1}{2}}$.
- Rewrite $\sqrt{10}$ as $\sqrt{1 + 9}$. Let $x = 9$.
- The binomial expansion is:
$$(1 + x)^{\frac{1}{2}} = 1 + \frac{1}{2}x + \frac{1}{2} \left( \frac{1}{2} - 1 \right) \frac{x^2}{2!} + \frac{1}{2} \left( \frac{1}{2} - 1 \right)\left( \frac{1}{2} - 2 \right) \frac{x^3}{3!} + \ldots$$
-
Evaluate Each Term for $x = 9$
- Substitute $x = 9$ into each term of the expansion:
$$ \sqrt{10} \approx 1 + \frac{1}{2}(9) + \frac{1}{2} \left( -\frac{1}{2} \right) \frac{9^2}{2} + \frac{1}{2} \left( -\frac{1}{2} \right)\left( -\frac{3}{2} \right) \frac{9^3}{6} $$
-
Calculate Individual Terms Simplify each term:
- ( 1 + \frac{9}{2} - \frac{9^2}{8} + \frac{27 \cdot 9^3}{48} )
- Calculate each value step-by-step.
The total number of ways the boys and girls can be seated is $10,080$.
The approximation for $\sqrt{10}$, using the series expansion, is approximately $3.16$ (after calculating each term).
More Information
- For the seating arrangement, treating the girls as a block simplifies the problem into arranging distinct units.
- The expansion of $(1 + x)^{\frac{1}{2}}$ is key in approximating square roots using Taylor series or binomial series.
Tips
- A common mistake is forgetting to treat the 2 girls as a single entity initially, causing an incorrect count of arrangements.
- In series expansions, it's important to correctly apply the binomial coefficients and simplify each term carefully.
AI-generated content may contain errors. Please verify critical information