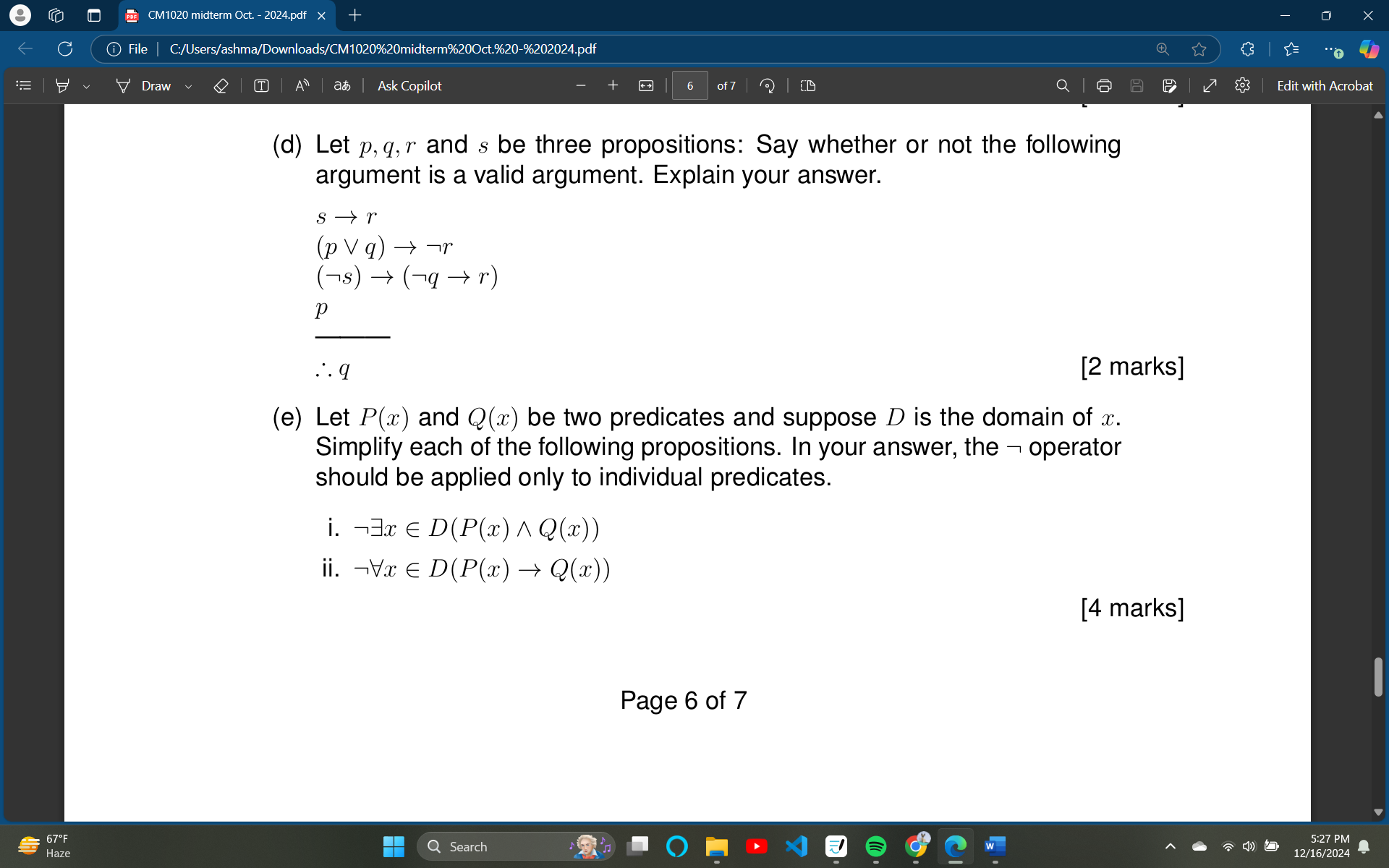
(d) Let p, q, r, and s be three propositions: Say whether or not the following argument is a valid argument. Explain your answer. s → r (p ∨ q) → ¬r (¬s) → (¬q → r) p ∴ q (e) Le... (d) Let p, q, r, and s be three propositions: Say whether or not the following argument is a valid argument. Explain your answer. s → r (p ∨ q) → ¬r (¬s) → (¬q → r) p ∴ q (e) Let P(x) and Q(x) be two predicates and suppose D is the domain of x. Simplify each of the following propositions. In your answer, the ¬ operator should be applied only to individual predicates. i. ¬∃x ∈ D(P(x) ∧ Q(x)) ii. ¬∀x ∈ D(P(x) → Q(x)) Read more

Steps to Solve

1. Check Validity of Argument

We need to examine whether the argument is valid. An argument is valid if, whenever the premises are true, the conclusion must also be true.

The premises are:

1. $s \rightarrow r$
2. $(p \vee q) \rightarrow \neg r$
3. $(\neg s) \rightarrow (\neg q \rightarrow r)$

And the conclusion is:

• $p \vdash q$

2. Analyze Premise Implications

From the premise $s \rightarrow r$, if $s$ is true, then $r$ must be true.

If we assume $s$ is false (which makes the first premise true, as false $\rightarrow$ anything is true), we can explore the implications of the other premises.

3. Using Premise 2

Premise 2 states $(p \vee q) \rightarrow \neg r$. If $r$ is true, then $\neg r$ must be false. Hence, either $p$ or $q$ must be false. We can denote:

• If $p$ is true, this forces $\neg r$ to be true.

4. Consider Premise 3

For premise 3, $(\neg s) \rightarrow (\neg q \rightarrow r)$, if $s$ is false, we have $(\neg q \rightarrow r)$. If $\neg q$ is true, then $q$ must be false, leading $r$ to be forced into truth.

Now, if we've created situations where $q$ must be both true and false without logical contradiction, we question the validity.

5. Conclusion of Validity

After analyzing the relationships created by the premises, we find the premises do not logically support the conclusion $q$. The argument is not valid.

6. Negate Predicates

For part (e), we simplify the two propositions:

1. For Part (i)

Given:

$$ \neg \exists x \in D (P(x) \land Q(x)) $$

Using the rule that $\neg \exists x P(x)$ is equivalent to $\forall x \neg P(x)$:

$$ \forall x \in D \neg (P(x) \land Q(x)) $$

By De Morgan's Law, this can be expressed as:

$$ \forall x \in D (\neg P(x) \vee \neg Q(x)) $$

2. For Part (ii)

Given:

$$ \neg \forall x \in D (P(x) \rightarrow Q(x)) $$

Using the rule that $\neg \forall x P(x)$ is equivalent to $\exists x \neg P(x)$:

$$ \exists x \in D \neg (P(x) \rightarrow Q(x)) $$

Using the implication equivalence, we have $P(x) \rightarrow Q(x) \equiv \neg P(x) \vee Q(x)$. Thus, it can be expressed as:

$$ \exists x \in D (P(x) \land \neg Q(x)) $$