Understand the Problem
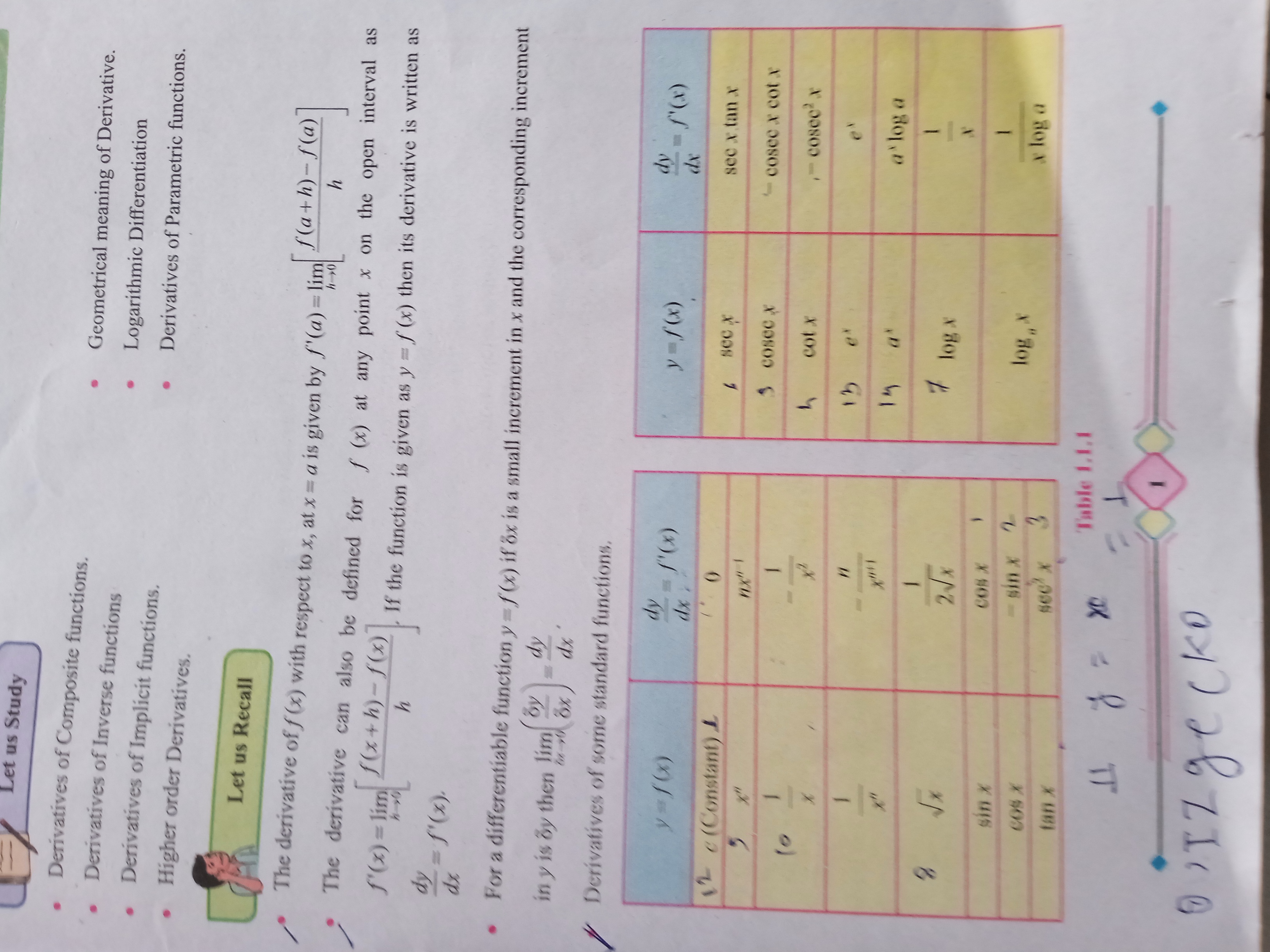
The image contains information related to derivatives, including definitions and a table of derivatives for various functions. It discusses the geometric meaning of derivatives and provides formulas for calculating them, focusing on parametric functions and logarithmic differentiation.
Answer
The derivative can be found by using the derivative table and applying the relevant rules. Provide a specific function for a direct answer.
Answer for screen readers
The answer will depend on the specific function you're working with. So, if you provide a specific function, I can give its derivative.
Steps to Solve
-
Identify the Function Type Determine whether the function in question is a standard type, such as polynomial, trigonometric, or logarithmic, as the table provides derivatives for various functions.
-
Use the Derivative Table Refer to the table of derivatives provided in the image. Locate the row that corresponds to your function.
-
Write the Derivative Write down the derivative based on the information in the table, ensuring you format it correctly.
-
Apply Chain Rule if Necessary If the function involves a composition of functions (like $f(g(x))$), apply the chain rule. The derivative of $y = f(g(x))$ is given by: $$ \frac{dy}{dx} = f'(g(x)) \cdot g'(x) $$
-
Check for Simplifications After calculating the derivative, simplify it if possible to get the final expression.
The answer will depend on the specific function you're working with. So, if you provide a specific function, I can give its derivative.
More Information
Derivatives are fundamental in calculus, representing the rate at which a function changes. They have vast applications in physics, engineering, and economics, among other fields.
Tips
- Forgetting to apply the chain rule: When dealing with composite functions, always remember to use the chain rule.
- Misreading the derivative table: Ensure you’re looking at the correct function category to avoid mistakes.
AI-generated content may contain errors. Please verify critical information