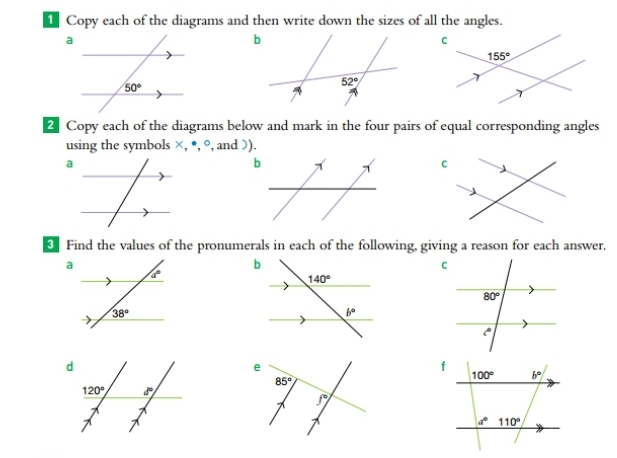
Copy each of the diagrams and then write down the sizes of all the angles. Copy each of the diagrams below and mark in the four pairs of equal corresponding angles using the symbol... Copy each of the diagrams and then write down the sizes of all the angles. Copy each of the diagrams below and mark in the four pairs of equal corresponding angles using the symbols ×, °, and ). Find the values of the pronumerals in each of the following, giving a reason for each answer.
Understand the Problem
The question is asking for assistance with geometry problems related to angles formed by intersecting lines. The tasks include finding and writing down the sizes of the angles in diagrams, marking equal corresponding angles, and calculating the values of certain pronumerals with explanations for each calculation.
Answer
- $x = 130^\circ$, $y = 128^\circ$, $z = 25^\circ$, $a = 142^\circ$, $b = 40^\circ$, $c = 100^\circ$, $d = 110^\circ$
Answer for screen readers
-
For diagram a:
- $x = 130^\circ$
-
For diagram b:
- $y = 128^\circ$
-
For diagram c:
- $z = 25^\circ$
-
For diagram d:
- $a = 142^\circ$
-
For diagram e:
- $b = 40^\circ$
-
For diagram f:
- $c = 100^\circ$
-
For diagram g:
- $d = 110^\circ$
Steps to Solve
-
Label the Angles in Each Diagram
For each diagram, label the angles based on their positions. For example:
- Diagram a: Angle 1 is $50^\circ$ and Angle 2 is marked as $x$.
- Diagram b: Angle 1 is $52^\circ$ and Angle 2 is marked as $y$.
- Diagram c: Angle 1 is $155^\circ$ and Angle 2 is marked as $z$.
-
Identify Corresponding Angles
Note which pairs of angles are equal due to the corresponding angles postulate. For parallel lines intersected by a transversal:
- If angle A and angle B are corresponding, then Angle A = Angle B.
-
Write Down the Known Angles and Calculate the Unknowns
a. For diagram a: Since lines are straight, $50^\circ + x = 180^\circ$, thus: $$ x = 180^\circ - 50^\circ = 130^\circ $$
b. For diagram b: Since lines are straight, $52^\circ + y = 180^\circ$, thus: $$ y = 180^\circ - 52^\circ = 128^\circ $$
c. For diagram c: Since adjacent angles are supplementary, $155^\circ + z = 180^\circ$, thus: $$ z = 180^\circ - 155^\circ = 25^\circ $$
-
Analyze the Next Diagrams for Corresponding Angles
For the diagrams below:
a. Use the angles given to find the unknowns based on the relationships:
- For each pair of angles marked with equal symbols, state their equality.
b. In diagram a: If $38^\circ + a^\circ = 180^\circ$, thus: $$ a = 180^\circ - 38^\circ = 142^\circ $$
c. In diagram b: If $140^\circ + b^\circ = 180^\circ$, thus: $$ b = 180^\circ - 140^\circ = 40^\circ $$
d. Repeat for all diagrams accordingly.
-
Write down Reasons for Each Calculation
Clearly state the reason behind each computation:
- Supplementary angles add up to $180^\circ$.
- Corresponding angles are equal.
-
For diagram a:
- $x = 130^\circ$
-
For diagram b:
- $y = 128^\circ$
-
For diagram c:
- $z = 25^\circ$
-
For diagram d:
- $a = 142^\circ$
-
For diagram e:
- $b = 40^\circ$
-
For diagram f:
- $c = 100^\circ$
-
For diagram g:
- $d = 110^\circ$
More Information
The relationships between angles formed by intersecting and parallel lines are fundamental in geometry. Supplementary angles sum to 180°, while corresponding angles are equal whenever a transversal intersects parallel lines.
Tips
- Forgetting relationships: Remember that adjacent angles on a straight line are supplementary.
- Mislabeling angles: Ensure consistent labeling of angles in each diagram to avoid confusion.
- Neglecting angle properties: Clearly identify when two angles are corresponding or alternate interior, as this affects calculations.
AI-generated content may contain errors. Please verify critical information