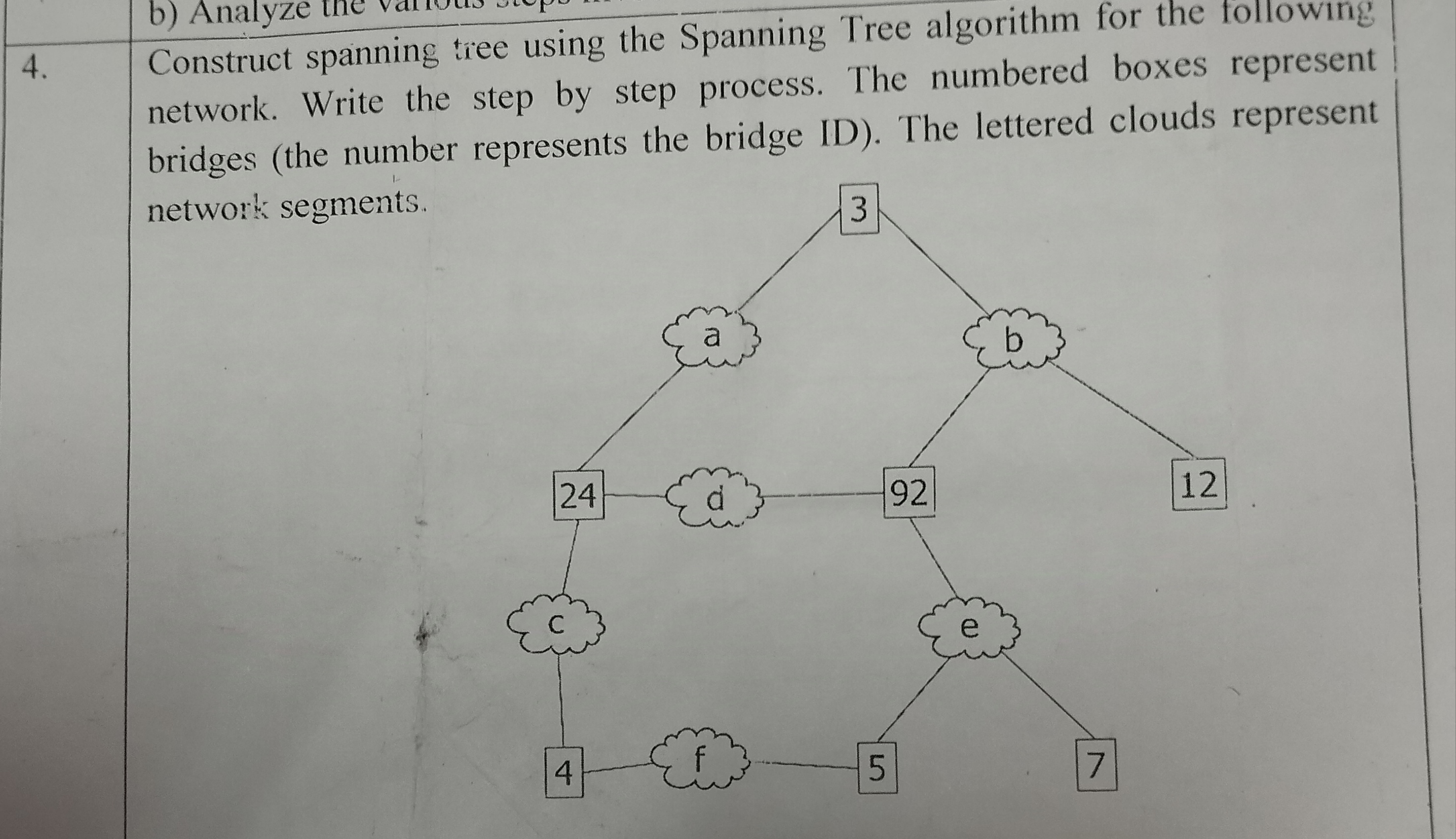
Construct a spanning tree using the Spanning Tree algorithm for the following network. Write the step by step process. The numbered boxes represent bridges (the number represents t... Construct a spanning tree using the Spanning Tree algorithm for the following network. Write the step by step process. The numbered boxes represent bridges (the number represents the bridge ID). The lettered clouds represent network segments.
Understand the Problem
The question is asking to construct a spanning tree using the Spanning Tree algorithm for a given network diagram. It requires a step-by-step explanation of the process, focusing on the numbered boxes representing bridges and the lettered clouds representing network segments.
Answer
The edges in the spanning tree are (3, a, b), (4, c, f), (5, e, f), (7, e, d), (12, d, b).
Answer for screen readers
The edges in the spanning tree are:
- (3, a, b)
- (4, c, f)
- (5, e, f)
- (7, e, d)
- (12, d, b)
Steps to Solve
- Identify the Bridges and Their Weights
From the diagram, identify the bridges (the numbered boxes) and their connections. The bridges are associated with the following weights:
- Bridge (3, a, b)
- Bridge (24, d, a)
- Bridge (92, d, b)
- Bridge (12, b, d)
- Bridge (4, c, f)
- Bridge (5, e, f)
- Bridge (7, e, d)
- List the Edges and Sort by Weight
List all edges with their weights and sort them in ascending order:
- (3, a, b)
- (4, c, f)
- (5, e, f)
- (7, e, d)
- (12, d, b)
- (24, d, a)
- (92, d, b)
- Apply Kruskal's Algorithm
Start building the spanning tree by taking the edges in order of increasing weight while avoiding cycles:
- Add edge (3, a, b)
- Add edge (4, c, f)
- Add edge (5, e, f)
- Add edge (7, e, d)
- Add edge (12, d, b)
- Check for Cycles
After adding edges, check for any cycles. Since no cycles are formed with the edges added, continue.
- Construct the Final Spanning Tree
The final spanning tree consists of the selected edges:
- (3, a, b)
- (4, c, f)
- (5, e, f)
- (7, e, d)
- (12, d, b)
The edges in the spanning tree are:
- (3, a, b)
- (4, c, f)
- (5, e, f)
- (7, e, d)
- (12, d, b)
More Information
The spanning tree constructed using the edges has a total minimum weight, ensuring that all nodes are connected without forming cycles. The edges selected follow the minimum spanning tree properties of Kruskal's algorithm.
Tips
- Forgetting to Check for Cycles: When adding edges, always ensure that no cycles are formed. Sometimes edge addition can accidentally lead to cycles.
- Not Sorting the Edges Correctly: Failure to sort edges by weight before processing can lead to incorrect spanning trees.
AI-generated content may contain errors. Please verify critical information