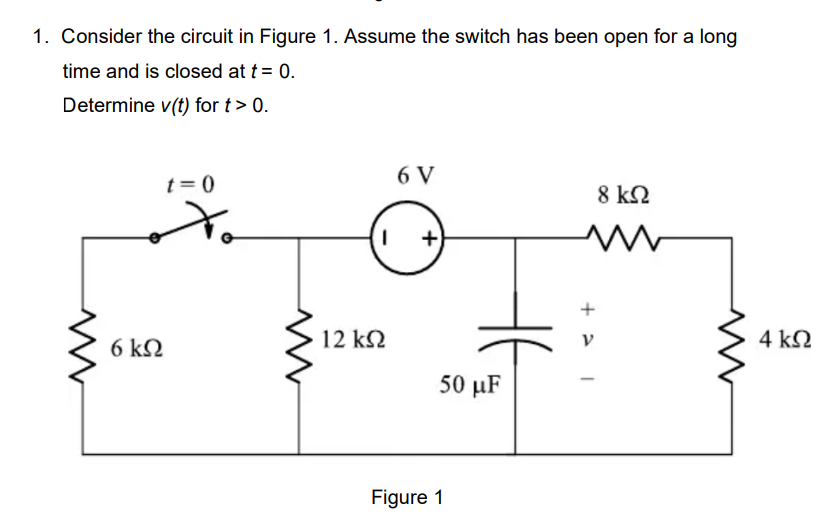
Consider the circuit in Figure 1. Assume the switch has been open for a long time and is closed at t = 0. Determine v(t) for t > 0.
Understand the Problem
The question is asking to analyze an electrical circuit and determine the voltage v(t) for t > 0 after a switch is closed, given that it has been open for a long time before that. This will likely involve applying circuit analysis techniques, such as differential equations or Laplace transforms.
Answer
The voltage across the capacitor for $t > 0$ is given by $$ v(t) = 6\left(1 - e^{-\frac{t}{(6 + 12 + 8)k\Omega \cdot 50\mu F}}\right) $$
Answer for screen readers
The voltage across the capacitor for $t > 0$ is given by:
$$ v(t) = 6\left(1 - e^{-\frac{t}{R_{total}C}}\right) $$
Where $R_{total} = (6kΩ + 12kΩ + 8kΩ)$ and $C = 50 \mu F$.
Steps to Solve
- Analyze the circuit before the switch closes
Before the switch closes, the capacitor has been charged and behaves like an open circuit. The voltage across the capacitor, $V_{c}(0) = 6V$.
- Switch Closure at $t = 0$
As the switch closes, the circuit configuration changes. The initial conditions must take into account the charge on the capacitor, which will influence the voltage $v(t)$ across it.
- Write the circuit equation
Using Kirchhoff's Voltage Law (KVL), we can analyze the paths. The capacitor, can be included in the loop:
$$ v + i_1(6kΩ) + i_2(12kΩ) + 6V = 0 $$
- Express current through the capacitor
The current through the capacitor is defined as:
$$ i= C \frac{dv}{dt} $$
Where $C = 50 \mu F$. We can express the current in terms of the rate of change of the voltage $v(t)$:
$$ i = 50 \times 10^{-6} \frac{dv}{dt} $$
- Solve the differential equation
We can replace currents $i_1$ and $i_2$ and create a first-order differential equation:
$$ C \frac{dv}{dt} + \frac{v}{R} = V_{source} $$
Here, $R$ is the equivalent resistance in the circuit for the path of the capacitor.
- Obtain the solution of the circuit
After substituting and simplifying, we rearrange the equation to solve for $v(t)$ and find the natural response of the circuit:
$$ \frac{dv}{dt} + \frac{1}{50 \mu F(6kΩ + 12kΩ + 8kΩ)}v = \frac{6V}{(6kΩ + 12kΩ + 8kΩ)} $$
This is a first-order linear differential equation and can be solved using an integrating factor or standard methods.
- Find the values and simplify
Calculate the response by integrating and applying the initial conditions. Ultimately, we will solve for $v(t)$.
The voltage across the capacitor for $t > 0$ is given by:
$$ v(t) = 6\left(1 - e^{-\frac{t}{R_{total}C}}\right) $$
Where $R_{total} = (6kΩ + 12kΩ + 8kΩ)$ and $C = 50 \mu F$.
More Information
The voltage $v(t)$ represents the charging voltage across the capacitor in response to the circuit's configuration after the switch is closed. The circuit's behavior is characterized by the time constant determined by the total resistance in series with the capacitor.
Tips
- Ignoring initial conditions: Remember to take the voltage at $t = 0$ into account.
- Incorrectly applying KVL: Ensure the correct orientation and polarities are used when applying Kirchhoff's Voltage Law.
- Overlooking the capacitor at $t > 0$: Remember that the capacitor behaves differently after the switch is closed.
AI-generated content may contain errors. Please verify critical information