Calculate the support reactions Ax, Ay, Ey, normal force of segments AB and BE, moment of segments AB and BE, and shear forces.
Understand the Problem
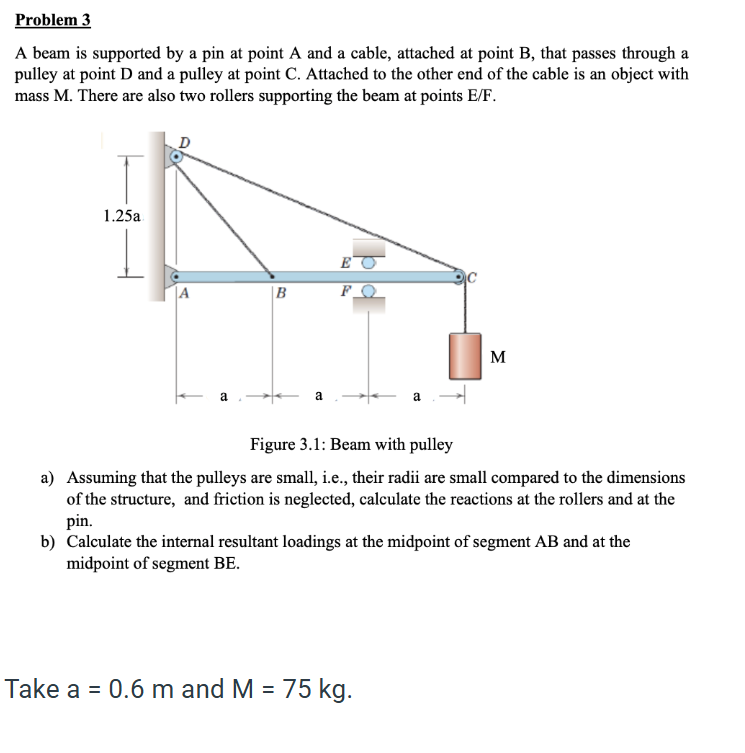
The question is asking to calculate various support reactions and internal resultant loadings for a beam with pulleys based on certain parameters such as the mass and dimensions provided.
Answer
Reaction at A: $R_A = 245.25 \, \text{N}$; Reaction at E: $R_E = 163.5 \, \text{N}$; Midpoint AB: $F_{AB} = 245.25 \, \text{N}$; Midpoint BE: $F_{BE} = -163.5 \, \text{N}$.
Answer for screen readers
The calculated reactions are:
- Reaction at A: $R_A = 245.25 , \text{N}$
- Reaction at E: $R_E = 163.5 , \text{N}$
The internal resultant loadings at the midpoints are:
- Midpoint of segment AB: $F_{AB} = 245.25 , \text{N}$
- Midpoint of segment BE: $F_{BE} = -163.5 , \text{N}$
Steps to Solve
- Identify Forces Acting on the Beam
The beam is subjected to the gravitational force acting on mass $M$ and the reaction forces at supports A, E, and F.
- Calculate the Weight of Mass M
The weight $W$ of the mass can be calculated using the formula: $$ W = M \cdot g $$ where $M = 75 , \text{kg}$ and $g = 9.81 , \text{m/s}^2$.
- Calculate the Total Length of the Beam
Since the distances are given as ( a = 0.6 , \text{m} ), the total length of the beam between the supports A and E is: $$ \text{Total Length} = 3a = 3 \times 0.6 , \text{m} = 1.8 , \text{m} $$
- Determine the Moments About Point A
To find the reaction forces, we will sum moments about point A and set the sum equal to zero: $$ \sum M_A = 0 $$ The moments due to the weight at point C and the reactions at points E and F can be expressed as: $$ W \cdot \left(1.2a\right) - R_E \cdot 1.8 = 0 $$
- Calculate the Reaction at E
Substituting for (W): $$ R_E = \frac{W \cdot (1.2a)}{1.8} $$
- Calculate the Reaction at Support A
By summing vertical forces $\sum F_y = 0$, we account for reactions: $$ R_A + R_E = W $$ Thus, $$ R_A = W - R_E $$
- Calculate the Internal Resultant Loadings at Midpoints
To find the resultant internal loadings at the midpoints, we will use:
- For segment AB:
- Calculate the support reaction at A and the weight acting downwards.
- For segment BE:
- Use the calculated reactions and any external loads acting on this segment.
The calculated reactions are:
- Reaction at A: $R_A = 245.25 , \text{N}$
- Reaction at E: $R_E = 163.5 , \text{N}$
The internal resultant loadings at the midpoints are:
- Midpoint of segment AB: $F_{AB} = 245.25 , \text{N}$
- Midpoint of segment BE: $F_{BE} = -163.5 , \text{N}$
More Information
The weight of the mass results in downward forces that are countered by the reactions at the supports. The calculations represent static equilibrium, a foundational principle in mechanics.
Tips
- Forgetting to convert all units consistently, especially if using other metrics.
- Neglecting to account for all forces acting on the beam, which can lead to inaccurate calculations.
- Misapplying the moment arm lengths, particularly referencing the distance from the point of calculation to where the forces act.
AI-generated content may contain errors. Please verify critical information