1) Verify the equality: 2(x - 3)(x + 7) = 2x^2 + 8x - 42. 2) Solve the equation 2x^2 + 8x - 42 = 0.
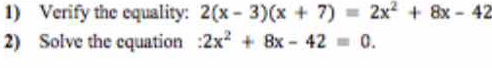
Understand the Problem
The question consists of two parts. The first part asks to verify the equality of two polynomial expressions by expanding the left side and checking if it equals the right side. The second part requires solving a quadratic equation set to zero.
Answer
The solutions are $x = -7$ and $x = 3$.
Answer for screen readers
The solutions to the quadratic equation are $x = -7$ and $x = 3$.
Steps to Solve
- Expand the Left Side of the Equation
Start by expanding the left side: $2(x - 3)(x + 7)$.
First, expand the binomials: $$(x - 3)(x + 7) = x^2 + 7x - 3x - 21 = x^2 + 4x - 21$$
Now, multiply this result by 2: $$2(x^2 + 4x - 21) = 2x^2 + 8x - 42$$
- Compare Both Sides
Now compare the expanded form from the left side with the right side: $$2x^2 + 8x - 42 = 2x^2 + 8x - 42$$
Since both expressions are equal, the first part is verified.
- Set Up the Quadratic Equation
Next, we solve the quadratic equation given: $$2x^2 + 8x - 42 = 0$$
- Simplify the Equation
Divide the entire equation by 2 for easier calculations: $$x^2 + 4x - 21 = 0$$
- Factor the Quadratic
Now, we need to factor the quadratic: $$(x + 7)(x - 3) = 0$$
- Find the Solutions
Set each factor to zero: $$x + 7 = 0 \quad \text{or} \quad x - 3 = 0$$
This gives us: $$x = -7 \quad \text{or} \quad x = 3$$
The solutions to the quadratic equation are $x = -7$ and $x = 3$.
More Information
The first part of the problem confirmed the equality of the two polynomial expressions. The second part reveals the roots of the quadratic equation. Understanding these roots can help in graphing the function or finding maximums and minimums.
Tips
- Forgetting to distribute correctly in the first step when expanding.
- Not checking if the roots found satisfy the original quadratic equation.
- Failing to simplify the equation when possible.
AI-generated content may contain errors. Please verify critical information