Calculate the area of the kite.

Understand the Problem

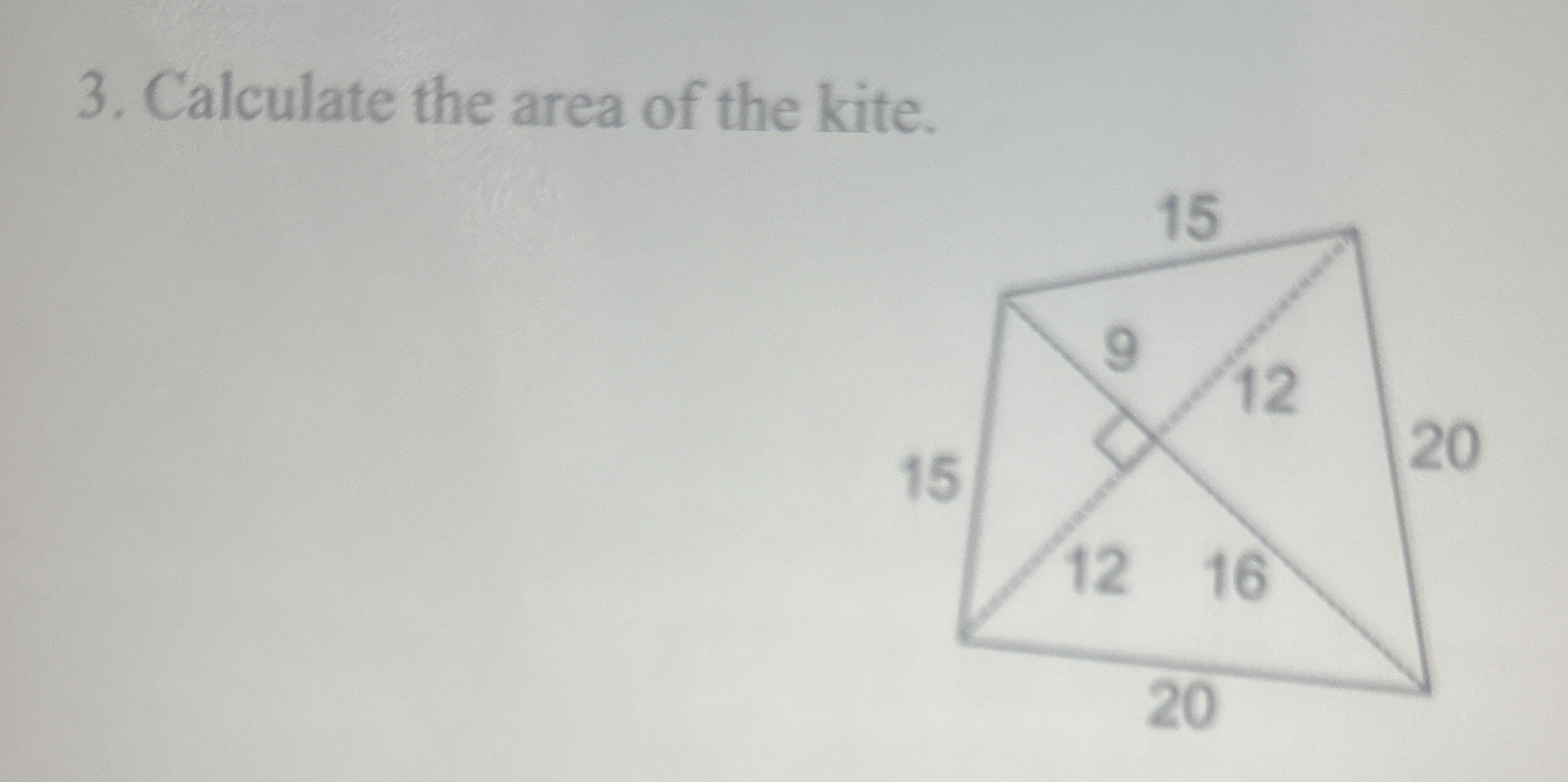
The question is asking to calculate the area of a kite, using the given dimensions in the diagram. The area of a kite can be calculated using the formula A = (d1 * d2) / 2, where d1 and d2 are the lengths of the diagonals.

Answer

The area of the kite is $480$ square units.

Steps to Solve

Identify the lengths of the diagonals

From the diagram, we can observe the diagonals of the kite. The diagonals are represented as:

$d_1 = 12 + 12 = 24$
$d_2 = 9 + 15 + 16 = 40$

Use the area formula for a kite

The area $A$ of a kite is given by the formula:

$$ A = \frac{d_1 \times d_2}{2} $$

Substituting the values of the diagonals into the formula:

Calculate the area of the kite

Now plug in the values for $d_1$ and $d_2$:

$$ A = \frac{24 \times 40}{2} $$

Calculating this gives:

$$ A = \frac{960}{2} = 480 $$

The area of the kite is $480$ square units.

More Information

The area of a kite can be quickly calculated using the diagonals, making it a handy formula in geometry. Kites have distinct properties, notably that their diagonals are perpendicular, which is critical in applications of the area formula.

Tips

Confusing the lengths of the diagonals. Ensure to correctly sum the segments that make up each diagonal.
Forgetting to divide by 2 in the area formula. Always remember this step when using the formula.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!