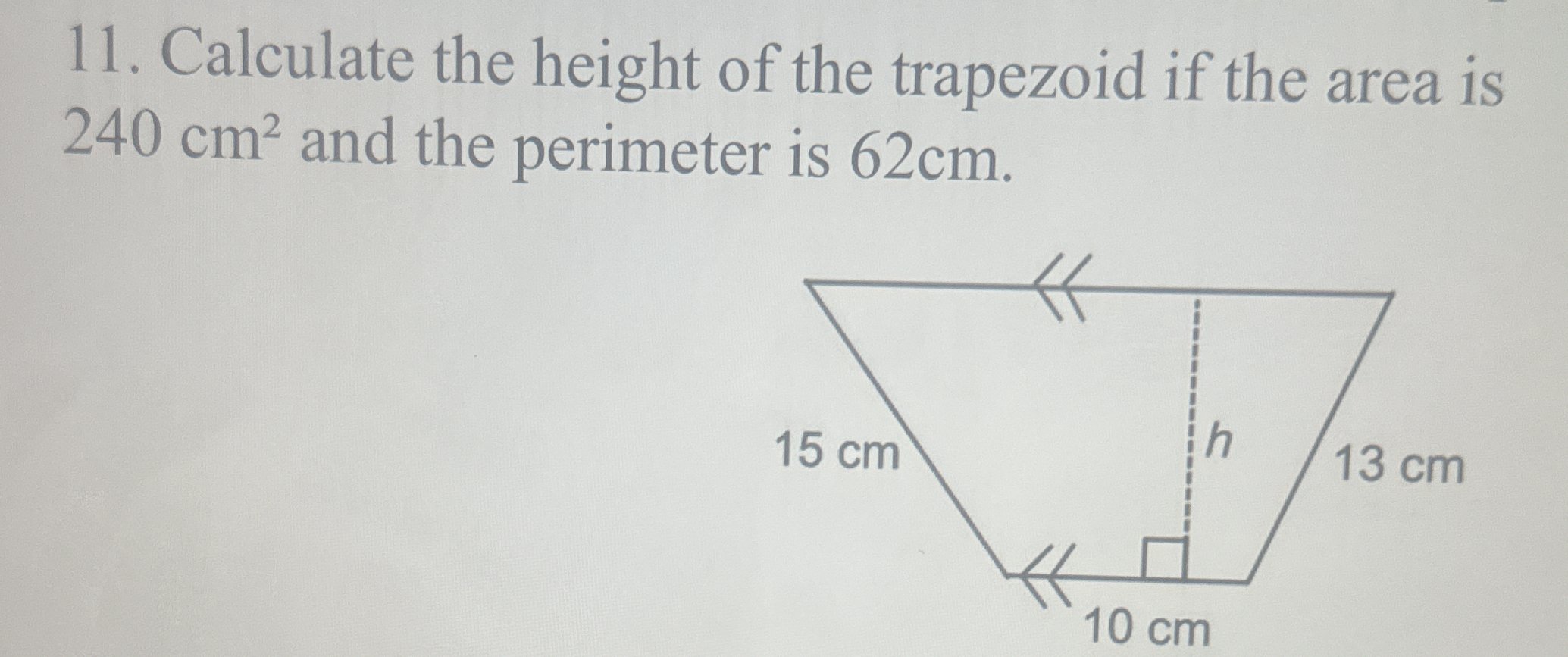
Calculate the height of the trapezoid if the area is 240 cm² and the perimeter is 62 cm.

Steps to Solve

1. Identify Given Values The area of the trapezoid is given as $A = 240 , \text{cm}^2$ and the perimeter as $P = 62 , \text{cm}$. The lengths of the bases are $b_1 = 10 , \text{cm}$ and $b_2 = 15 , \text{cm}$.

2. List the Perimeter Formula The perimeter of a trapezoid is calculated using the formula: $$ P = b_1 + b_2 + l_1 + l_2 $$ where $l_1$ and $l_2$ are the lengths of the non-parallel sides.

3. Set Up the Perimeter Equation Substituting the known lengths into the equation: $$ 62 = 10 + 15 + l_1 + l_2 $$

4. Calculate the Sum of the Non-Parallel Sides Simplifying gives: $$ l_1 + l_2 = 62 - 25 = 37 $$

5. Identify and Substitute for Height Using the area formula for a trapezoid: $$ A = \frac{1}{2} (b_1 + b_2) h $$ Substitute the known values: $$ 240 = \frac{1}{2} (10 + 15) h $$

6. Solve for Height Calculating the base sum: $$ 10 + 15 = 25 $$ Then substituting: $$ 240 = \frac{1}{2} \cdot 25 \cdot h $$ $$ 240 = 12.5h $$

7. Isolate Height Dividing both sides by 12.5: $$ h = \frac{240}{12.5} $$

8. Calculate Height Perform the division: $$ h = 19.2 , \text{cm} $$