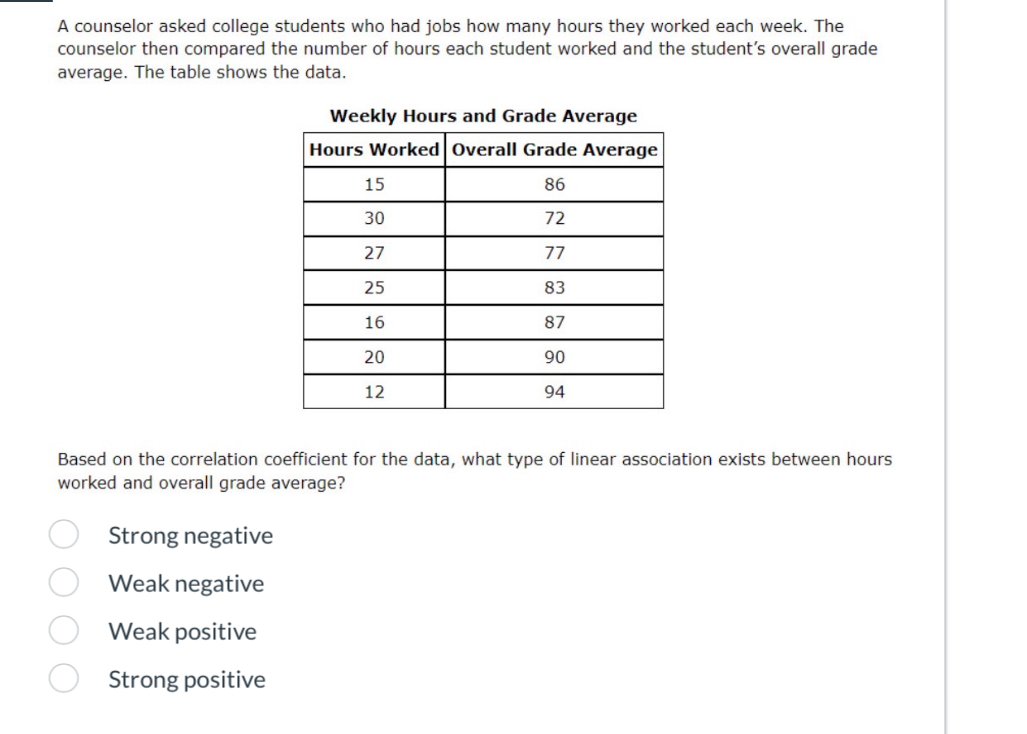
Based on the correlation coefficient for the data, what type of linear association exists between hours worked and overall grade average?

Steps to Solve

1. Organize the Data

   Create a list of the given data points for hours worked and overall grade average:

   • Hours Worked: ( [15, 30, 27, 25, 16, 20, 12] )
   • Overall Grade Average: ( [86, 72, 77, 83, 87, 90, 94] )

2. Calculate the Correlation Coefficient

   The formula for the correlation coefficient ( r ) is given by:

   $$ r = \frac{n(\sum xy) - (\sum x)(\sum y)}{\sqrt{[n \sum x^2 - (\sum x)^2][n \sum y^2 - (\sum y)^2]}} $$

   Where:

   • ( n ) is the number of pairs of scores
   • ( x ) represents the hours worked
   • ( y ) represents the overall grade average

3. Compute Individual Sums and Products

   Find the following sums:

   • ( \sum x = 15 + 30 + 27 + 25 + 16 + 20 + 12 = 145 )
   • ( \sum y = 86 + 72 + 77 + 83 + 87 + 90 + 94 = 519 )
   • ( \sum xy = (15)(86) + (30)(72) + (27)(77) + (25)(83) + (16)(87) + (20)(90) + (12)(94) = 1240 + 2160 + 2079 + 2075 + 1392 + 1800 + 1128 = 10974 )
   • ( \sum x^2 = 15^2 + 30^2 + 27^2 + 25^2 + 16^2 + 20^2 + 12^2 = 225 + 900 + 729 + 625 + 256 + 400 + 144 = 3279 )
   • ( \sum y^2 = 86^2 + 72^2 + 77^2 + 83^2 + 87^2 + 90^2 + 94^2 = 7396 + 5184 + 5929 + 6889 + 7569 + 8100 + 8836 = 40893 )

4. Substitute into the Correlation Formula

   Substitute the sums calculated into the correlation formula:

   [ r = \frac{7(10974) - (145)(519)}{\sqrt{[7(3279) - (145)^2][7(40893) - (519)^2]}} ] This calculates the value of ( r ).

5. Interpret the Correlation Coefficient

   Analyze the value of ( r ):

   • If ( r ) is close to 1, it indicates a strong positive correlation.
   • If ( r ) is close to -1, it indicates a strong negative correlation.
   • If ( r ) is around 0, it indicates no correlation.
   • We will determine which category (strong negative, weak negative, weak positive, strong positive) it falls into.