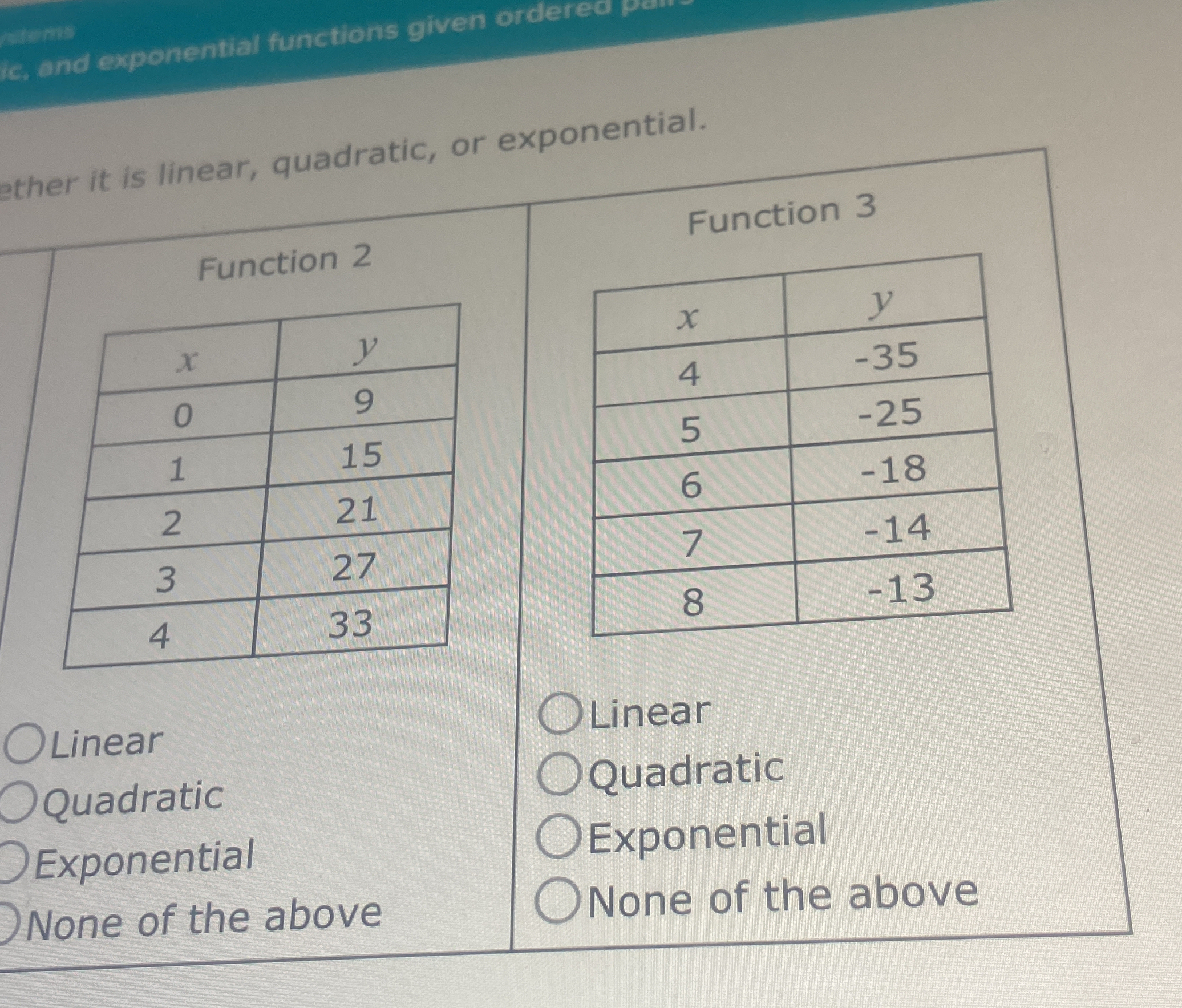
Determine whether Function 2 and Function 3 are linear, quadratic, or exponential based on the given ordered pairs.

Steps to Solve

1. Analyze Function 2 for Patterns

To determine if Function 2 is linear, quadratic, or exponential, look at the $y$ values:

• For $x = 0, y = 9$
• For $x = 1, y = 15$
• For $x = 2, y = 21$
• For $x = 3, y = 27$
• For $x = 4, y = 33$

Calculate the differences in $y$ values as $x$ increases:

• Difference when $x$ increases from $0$ to $1$: $15 - 9 = 6$
• Difference when $x$ increases from $1$ to $2$: $21 - 15 = 6$
• Difference when $x$ increases from $2$ to $3$: $27 - 21 = 6$
• Difference when $x$ increases from $3$ to $4$: $33 - 27 = 6$

The differences are constant, indicating a linear relationship.

2. Analyze Function 3 for Patterns

Now, analyze the $y$ values for Function 3:

• For $x = 4, y = -35$
• For $x = 5, y = -25$
• For $x = 6, y = -18$
• For $x = 7, y = -14$
• For $x = 8, y = -13$

Calculate the differences as $x$ increases:

• Difference when $x$ increases from $4$ to $5$: $-25 - (-35) = 10$
• Difference when $x$ increases from $5$ to $6$: $-18 - (-25) = 7$
• Difference when $x$ increases from $6$ to $7$: $-14 - (-18) = 4$
• Difference when $x$ increases from $7$ to $8$: $-13 - (-14) = 1$

The differences are not constant, so Function 3 isn't linear. Now compute the second differences:

• First differences: $10, 7, 4, 1$
• Second differences: $7 - 10 = -3$, $4 - 7 = -3$, $1 - 4 = -3$

The second differences are constant, indicating a quadratic relationship.