Assume that z = f(x, y)^2, x = g(t), y = h(t), f_y(1, 0) = 1, f_x(1, 0) = -1, f(1, 0) = 2. If g(3) = 1, h(3) = 0, g'(3) = -3, and h'(3) = 4, find dz/dt|_{t=3}.
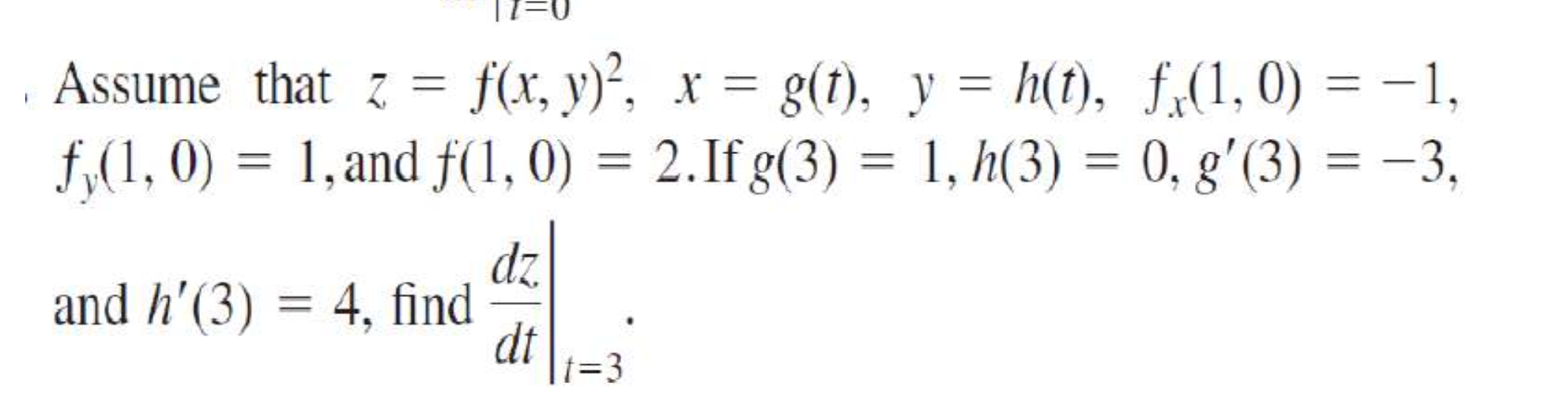
Understand the Problem
The question involves calculating the rate of change of z with respect to t at a specific point, given a multivariable function z and its dependencies on x and y, which are further defined as functions of t. The problem provides specific values and derivatives that must be utilized in applying the chain rule and implicit differentiation to find the desired rate of change.
Answer
The final answer is \( 7 \).
Answer for screen readers
The value of ( \frac{dz}{dt} \bigg|_{t=3} ) is ( 7 ).
Steps to Solve
-
Identify the multivariable function and its derivatives
Given that ( z = f(x, y)^2 ), ( x = g(t) ), and ( y = h(t) ), we will need to use the chain rule to differentiate ( z ) with respect to ( t ). We are given the derivatives ( f_x(1, 0), f_y(1, 0), g'(3), ) and ( h'(3) ) along with specific function values. -
Apply the Chain Rule
Using the chain rule, we can express ( \frac{dz}{dt} ) as follows:
$$ \frac{dz}{dt} = \frac{\partial z}{\partial x} \cdot \frac{dx}{dt} + \frac{\partial z}{\partial y} \cdot \frac{dy}{dt} $$
Substituting in the partial derivatives: $$ \frac{dz}{dt} = f_x(x,y) \cdot g'(t) + f_y(x,y) \cdot h'(t) $$ -
Evaluate at the specific point
At ( t = 3 ), we find:
- ( g(3) = 1 ) and ( h(3) = 0 )
thus, substituting ( x = 1 ) and ( y = 0 ): $$ \frac{dz}{dt} \bigg|_{t=3} = f_x(1, 0) \cdot g'(3) + f_y(1, 0) \cdot h'(3) $$ - The derivatives are given as ( f_x(1, 0) = -1 ), ( f_y(1, 0) = 1 ), ( g'(3) = -3 ), and ( h'(3) = 4 ).
-
Substituting values into the equation
Substituting these values into the equation: $$ \frac{dz}{dt} \bigg|_{t=3} = (-1)(-3) + (1)(4) $$ -
Calculate the final value
Calculating: $$ \frac{dz}{dt} \bigg|_{t=3} = 3 + 4 = 7 $$
The value of ( \frac{dz}{dt} \bigg|_{t=3} ) is ( 7 ).
More Information
This result illustrates how the rate of change of a multivariable function with respect to time can be computed using the chain rule, factoring in the contributions from each variable involved.
Tips
- Forgetting to evaluate the function and derivatives at the correct point ( (1, 0) ).
- Misapplying the chain rule can lead to incorrect expressions for ( \frac{dz}{dt} ). Make sure to differentiate correctly and account for all variables.
AI-generated content may contain errors. Please verify critical information