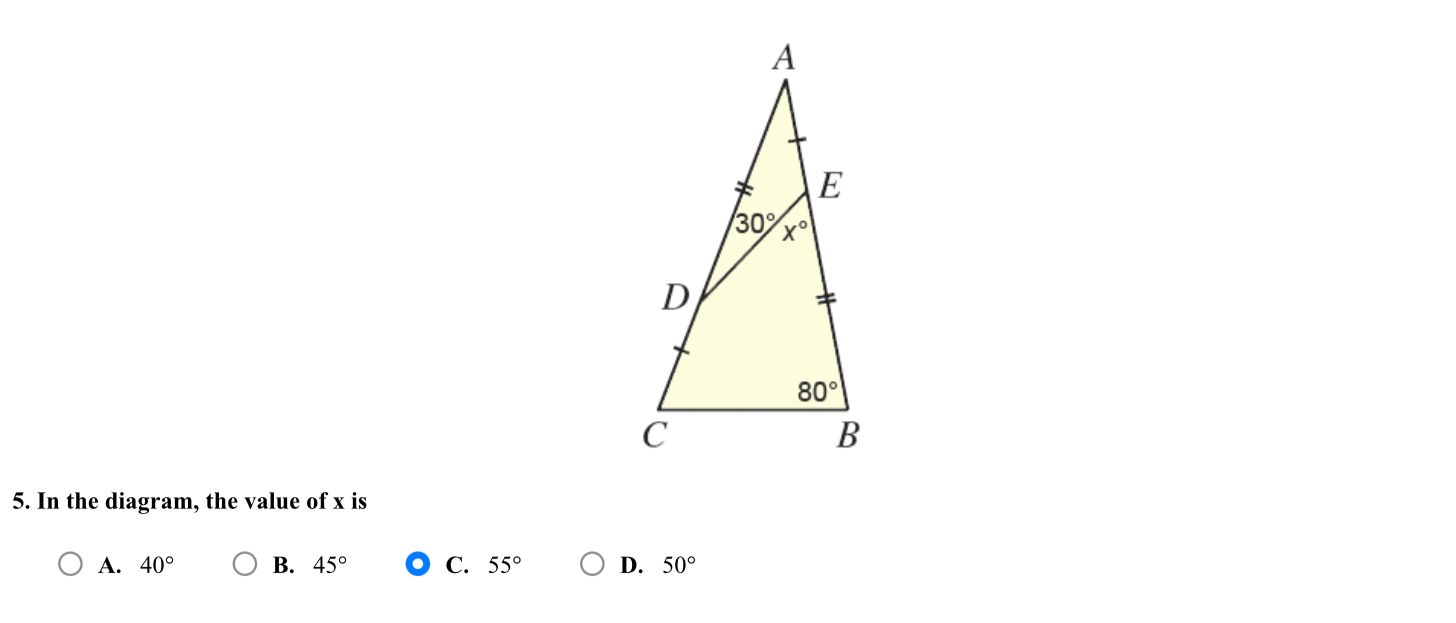
In the diagram, the value of x is
Understand the Problem
The question is asking to find the value of the angle x in the triangle, given other angles and the rules of triangle geometry. We will use the properties that the sum of the angles in a triangle is 180 degrees to solve for x.
Answer
The value of \( x \) is \( 70^\circ \).
Answer for screen readers
The value of ( x ) is ( 70^\circ ).
Steps to Solve
- Identify the known angles
In the triangle, we know two angles: $30^\circ$ and $80^\circ$.
- Apply the triangle sum theorem
The sum of the angles in a triangle is always $180^\circ$. Therefore, we can find the third angle $x$ using the equation:
$$ x + 30^\circ + 80^\circ = 180^\circ $$
- Calculate the value of x
Combine the known angles:
$$ 30^\circ + 80^\circ = 110^\circ $$
Now substitute into the equation:
$$ x + 110^\circ = 180^\circ $$
- Solve for x
Subtract $110^\circ$ from both sides:
$$ x = 180^\circ - 110^\circ $$
- Final calculation
This simplifies to:
$$ x = 70^\circ $$
The value of ( x ) is ( 70^\circ ).
More Information
In any triangle, the sum of all interior angles is always ( 180^\circ ). In this case, we used that property to find the missing angle. Be mindful that the diagram might not represent the angles correctly, this calculation is based solely on given values.
Tips
- Miscalculating the sum of the known angles.
- Forgetting to subtract from ( 180^\circ ) properly.
- Confusing the triangle properties with other polygon properties.
AI-generated content may contain errors. Please verify critical information