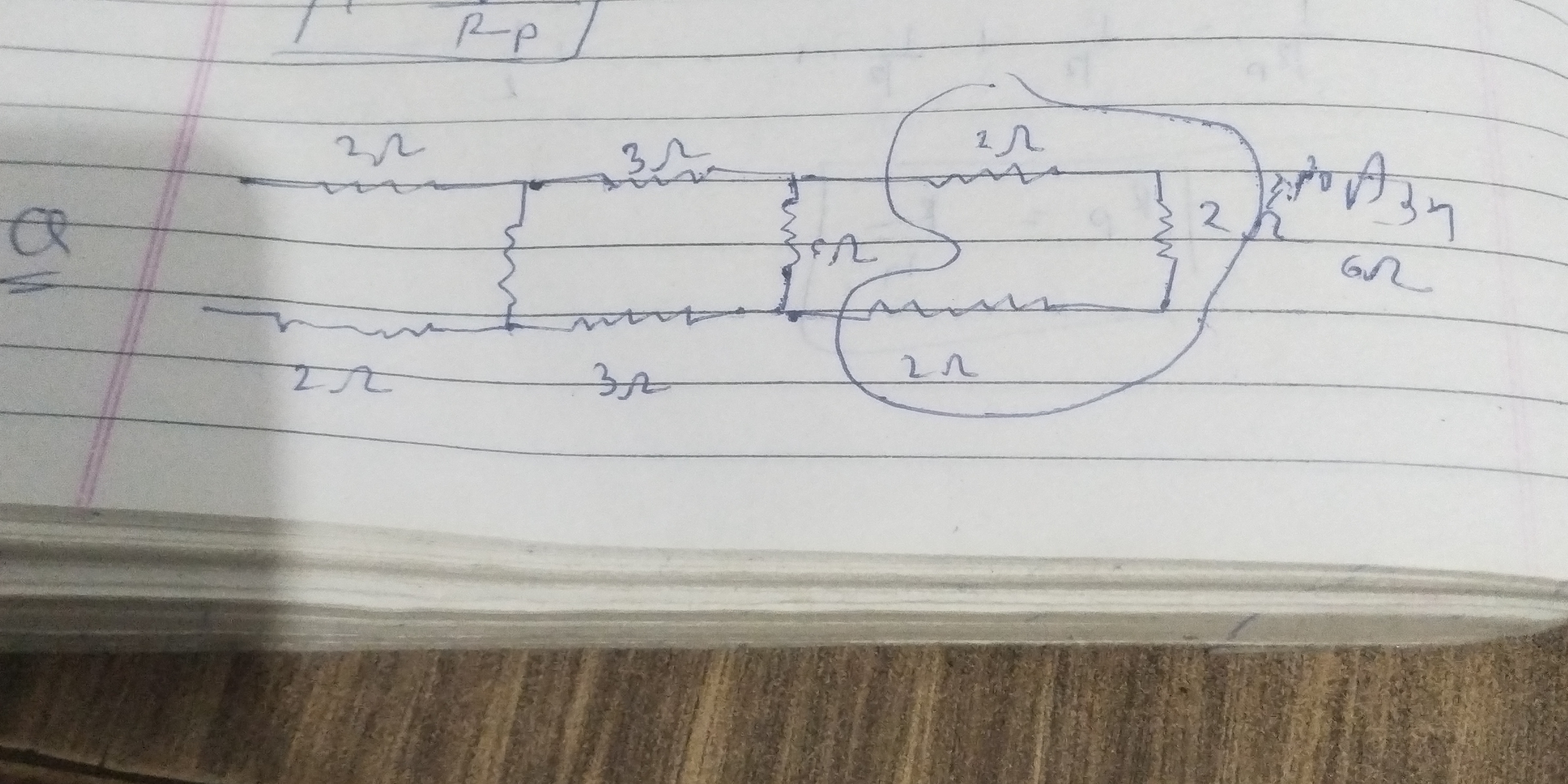
Analyze the electrical circuit shown in the image.

Steps to Solve

1. Identify the Components of the Circuit

The circuit consists of several resistors with values of $2 , \Omega$ and $3 , \Omega$. Observe how they are arranged in series and parallel.

2. Simplifying Resistors in Series and Parallel

For resistors in series, the equivalent resistance $R_s$ can be calculated using: $$ R_s = R_1 + R_2 + R_3 + \ldots $$

For resistors in parallel, the equivalent resistance $R_p$ can be calculated using: $$ \frac{1}{R_p} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots $$

3. Finding Equivalent Resistance Step by Step

• Combine the two $2 , \Omega$ resistors in series: $$ R_s = 2 , \Omega + 2 , \Omega = 4 , \Omega $$

• Next, find the equivalent resistance of the $4 , \Omega$ from above and the $3 , \Omega$ resistor in parallel: $$ \frac{1}{R_p} = \frac{1}{4 , \Omega} + \frac{1}{3 , \Omega} $$

Calculating this gives: $$ \frac{1}{R_p} = \frac{3 + 4}{12} = \frac{7}{12} \implies R_p = \frac{12}{7} , \Omega \approx 1.71 , \Omega $$

• Now, add this $R_p$ to the remaining $2 , \Omega$ resistor in series: $$ R_{\text{total}} = R_p + 2 , \Omega = \frac{12}{7} + 2 = \frac{12 + 14}{7} = \frac{26}{7} , \Omega $$

4. Final Calculation

Thus, the total equivalent resistance $R_{\text{total}}$ in the circuit is: $$ R_{\text{total}} = \frac{26}{7} , \Omega \approx 3.71 , \Omega $$