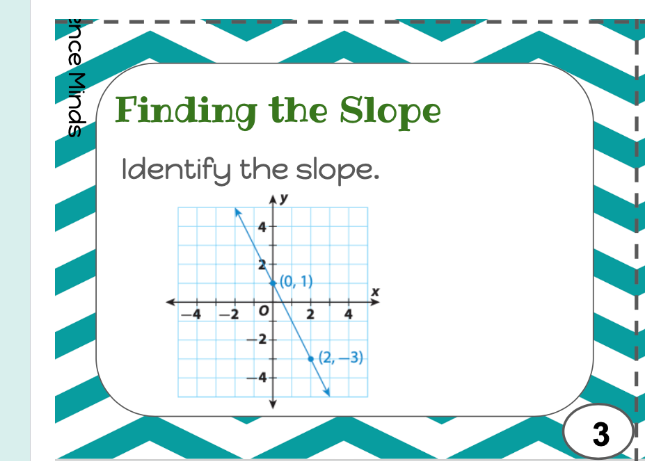
Identify the slope.
Understand the Problem
The question is asking to identify the slope of a line represented on a graph with two given points, (0, 1) and (2, -3). The slope can be calculated using the slope formula (change in y) / (change in x).
Answer
The slope is $m = -2$.
Answer for screen readers
The slope of the line is $m = -2$.
Steps to Solve
-
Identify the Points
We have two points from the graph:
Point 1: $(0, 1)$
Point 2: $(2, -3)$ -
Calculate Change in y
The change in $y$ is calculated as the difference in the $y$-coordinates of the two points:
$$ \Delta y = y_2 - y_1 = -3 - 1 = -4 $$ -
Calculate Change in x
The change in $x$ is calculated as the difference in the $x$-coordinates of the two points:
$$ \Delta x = x_2 - x_1 = 2 - 0 = 2 $$ -
Use the Slope Formula
The slope $m$ is calculated using the formula:
$$ m = \frac{\Delta y}{\Delta x} = \frac{-4}{2} $$ -
Simplify the Slope
Now simplify the slope:
$$ m = -2 $$
The slope of the line is $m = -2$.
More Information
The slope indicates that for every increase of 1 unit in the $x$-direction, the $y$-value decreases by 2 units. This means the line is decreasing as it moves from left to right.
Tips
-
Sign Errors: Neglecting to properly calculate the signs when finding $\Delta y$ and $\Delta x$. It's important to subtract the correct values.
-
Forgetting the Formula: Some may forget to use the slope formula properly. Always remember to divide the change in $y$ by the change in $x$.
AI-generated content may contain errors. Please verify critical information