a. What are the maximin, maximax, and equally likely decisions? b. Determine the best strategy, using expected monetary value (EMV), if you know that the market probabilities are 0... a. What are the maximin, maximax, and equally likely decisions? b. Determine the best strategy, using expected monetary value (EMV), if you know that the market probabilities are 0.4 for favorable market and 0.6 for unfavorable market. Read more

Steps to Solve

1. Identify Payoffs for Alternatives

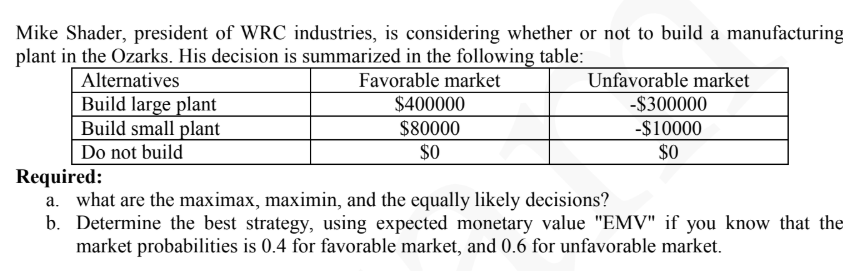
   From the table, we can summarize the payoffs of each alternative:

   • Build Large Plant: Favorable market: $400,000, Unfavorable market: -$300,000
   • Build Small Plant: Favorable market: $80,000, Unfavorable market: -$10,000
   • Do Not Build: $0 for both market conditions

2. Calculate Maximin Decision

   The maximin decision is found by identifying the worst-case scenario for each alternative and then choosing the best among those:

   • Build Large Plant: Worst case: $-300,000
   • Build Small Plant: Worst case: $-10,000
   • Do Not Build: Worst case: $0

   So, the maximin decision is: $$ \text{maximin} = \max(-300,000, -10,000, 0) = 0 $$

3. Calculate Maximax Decision

   The maximax decision considers the best outcome of each alternative:

   • Build Large Plant: Best case: $400,000
   • Build Small Plant: Best case: $80,000
   • Do Not Build: Best case: $0

   So, the maximax decision is: $$ \text{maximax} = \max(400,000, 80,000, 0) = 400,000 $$

4. Calculate Equally Likely Decision

   For the equally likely decision, we assume each market condition is equally probable (0.5 each). We calculate the average payoff for each alternative:

   • Build Large Plant: $$ \text{Expected} = \frac{1}{2}(400,000) + \frac{1}{2}(-300,000) = 50,000 $$
   • Build Small Plant: $$ \text{Expected} = \frac{1}{2}(80,000) + \frac{1}{2}(-10,000) = 35,000 $$
   • Do Not Build: $$ \text{Expected} = 0 $$

   The equally likely decision is: $$ \text{equally likely} = \max(50,000, 35,000, 0) = 50,000 $$

5. Calculate Expected Monetary Value (EMV)

   Using the given probabilities, we calculate the EMV for each alternative:

   • Build Large Plant: $$ \text{EMV} = (0.4 \times 400,000) + (0.6 \times -300,000) = 160,000 - 180,000 = -20,000 $$
   • Build Small Plant: $$ \text{EMV} = (0.4 \times 80,000) + (0.6 \times -10,000) = 32,000 - 6,000 = 26,000 $$
   • Do Not Build: $$ \text{EMV} = 0 $$

   The best strategy based on EMV is: $$ \text{Best EMV} = \max(-20,000, 26,000, 0) = 26,000 $$