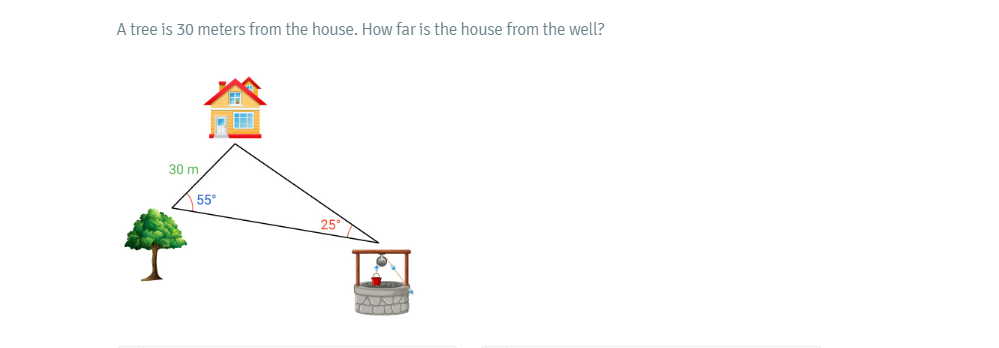
A tree is 30 meters from the house. How far is the house from the well?

Steps to Solve

1. Identify the triangle We have a triangle formed by the house, the tree, and the well. The distance from the house to the tree is 30 meters, the angle at the house is 55°, and the angle at the well is 25°.

2. Determine the third angle The sum of the angles in a triangle is always 180°. To find the third angle at the tree, we can calculate: $$ \text{Angle at tree} = 180° - 55° - 25° = 100° $$

3. Use the Law of Sines We can use the Law of Sines to find the distance from the house to the well, denoted as $b$. According to the Law of Sines: $$ \frac{a}{\sin(A)} = \frac{b}{\sin(B)} $$ Where:

• $a = 30 , \text{m}$ (distance from house to tree)
• $A = 25°$ (angle at the well)
• $B = 100°$ (angle at the tree)

4. Set up the equation We need to solve for $b$: $$ \frac{30}{\sin(25°)} = \frac{b}{\sin(100°)} $$

5. Solve for $b$ Rearranging gives us: $$ b = 30 \cdot \frac{\sin(100°)}{\sin(25°)} $$

6. Calculate sine values Using a calculator:

• $\sin(100°) \approx 0.9848$
• $\sin(25°) \approx 0.4226$

7. Substitute and solve Now substitute the sine values into the equation: $$ b = 30 \cdot \frac{0.9848}{0.4226} $$

8. Final calculation Calculating the above expression gives: $$ b \approx 69.78 , \text{meters} $$