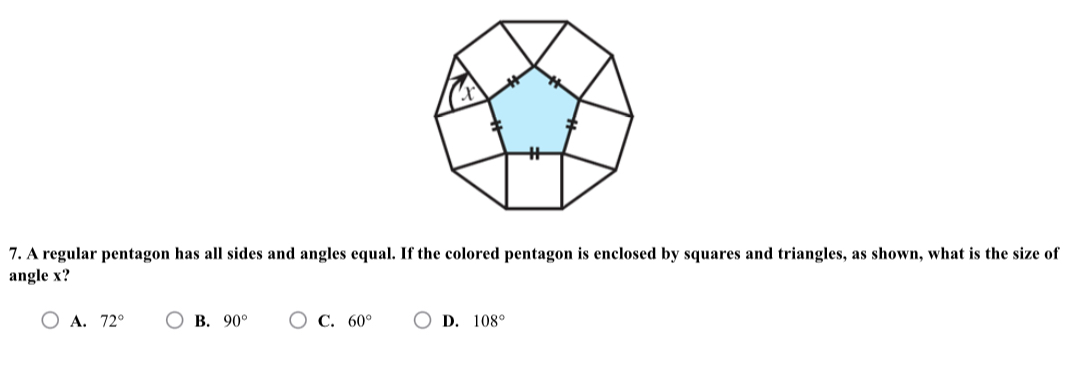
A regular pentagon has all sides and angles equal. If the colored pentagon is enclosed by squares and triangles, as shown, what is the size of angle x?
Understand the Problem
The question is asking for the measurement of angle x in a geometric figure that includes a regular pentagon, squares, and triangles. To solve it, we will need to apply knowledge of the properties of a regular pentagon and the relationships between the angles formed by the shapes surrounding it.
Answer
The measure of angle $x$ is $72^\circ$.
Answer for screen readers
The value of angle $x$ is $72^\circ$.
Steps to Solve
- Calculate the interior angle of the pentagon
A regular pentagon has 5 sides. The formula to calculate the interior angle of a regular polygon is given by:
$$ \text{Interior Angle} = \frac{(n - 2) \times 180^\circ}{n} $$
For a pentagon ($n = 5$):
$$ \text{Interior Angle} = \frac{(5 - 2) \times 180^\circ}{5} = \frac{3 \times 180^\circ}{5} = 108^\circ $$
- Analyze the triangle formed with the pentagon
In the figure, note that each vertex angle of the pentagon is 108°. The structure indicates that at each vertex of the pentagon, the exterior angles formed with the enclosing squares or triangles can help determine angle $x$.
- Determine angle x
Notice that in the case surrounding the vertex of the pentagon, there are supplementary angles formed by squares. Since the external angle at each vertex of the pentagon can also be computed by:
$$ \text{Exterior Angle} = 180^\circ - \text{Interior Angle} $$
Hence,
$$ \text{Exterior Angle} = 180^\circ - 108^\circ = 72^\circ $$
Since angle $x$ is vertically opposite to one of the angles that makes up this 72°, we conclude that $x$ must also equal 72°.
The value of angle $x$ is $72^\circ$.
More Information
In a regular pentagon, each interior angle is 108°. The exterior angle, which is supplementary to the interior angle, is thus 72°. Understanding angles in polygons, especially regular polygons, is crucial for these types of geometry problems.
Tips
- Confusing interior and exterior angles. Remember that the exterior angle is always supplementary to the interior angle.
- Not applying the correct polygon angle formulas. Ensuring the application of the appropriate formulas for regular polygons is important.
AI-generated content may contain errors. Please verify critical information