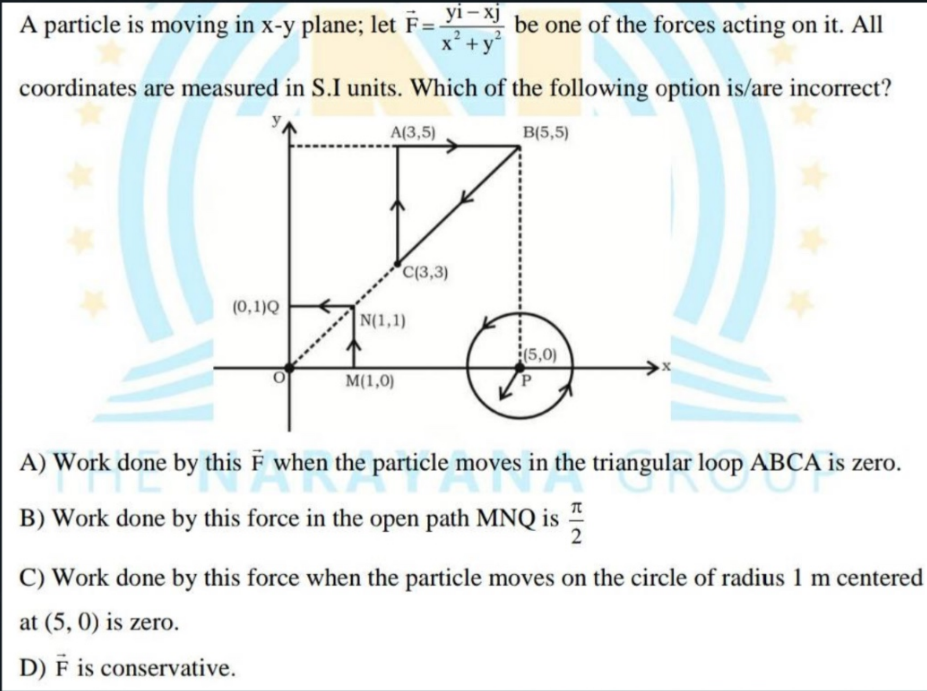
A particle is moving in the x-y plane; let F = (y/x^2 - x)j be one of the forces acting on it. All coordinates are measured in S.I. units. Which of the following option is/are inco... A particle is moving in the x-y plane; let F = (y/x^2 - x)j be one of the forces acting on it. All coordinates are measured in S.I. units. Which of the following option is/are incorrect? A) Work done by this F when the particle moves in the triangular loop ABC is zero. B) Work done by this force in the open path MNQ is π/2. C) Work done by this force when the particle moves on the circle of radius 1 m centered at (5, 0) is zero. D) F is conservative.
Understand the Problem
The question is asking about the work done by a force acting on a particle moving in the x-y plane. It presents four options regarding the work done in different paths and whether the force is conservative, and the task is to identify which of these options is incorrect.
Answer
D: $\vec{F}$ is conservative.
Answer for screen readers
The incorrect option is D: $\vec{F}$ is not conservative.
Steps to Solve
- Identify the Force Vector
We are given the force vector: $$ \vec{F} = \frac{y \hat{i} - x \hat{j}}{x^2 + y^2} $$
- Determine if the Force is Conservative
To check if the force is conservative, we can compute the curl of the force vector. A force is conservative if the curl is zero.
The curl in two dimensions can be calculated as: $$ \nabla \times \vec{F} = \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} $$
Where $F_x = \frac{y}{x^2 + y^2}$ and $F_y = -\frac{x}{x^2 + y^2}$.
- Calculate Partial Derivatives
We need to compute: $$ \frac{\partial F_y}{\partial x} = \frac{\partial}{\partial x} \left(-\frac{x}{x^2 + y^2}\right) $$ $$ \frac{\partial F_x}{\partial y} = \frac{\partial}{\partial y} \left(\frac{y}{x^2 + y^2}\right) $$
- Analyze the Results of the Curl
If the curl results in a non-zero value, the force is not conservative. If it equals zero, we can evaluate the given options.
- Evaluate Each Path
-
Loop ABC: The work done around a closed loop in a conservative field should be zero.
-
Open Path MN: The work done can be calculated using line integrals.
-
Circle at (5,0): Check if the work required to move in this circular path can be determined.
- Check Each Statement
Once the computations for the curl and work are done, compare results with the options:
A) Need to verify if it's zero. B) Calculate and verify the work done on path MN. C) Validate the work done on the path around the circle. D) Confirm whether the force is conservative.
The incorrect option is D: $\vec{F}$ is not conservative.
More Information
The force field provided has a singularity at the origin (0,0), causing the work done to be path-dependent in regions surrounding this point. This implies that the force is not conservative.
Tips
- Forgetting to check the area of singularity when determining if a force is conservative.
- Miscalculating the line integrals along paths, especially for open paths.
- Confusing conservative forces with non-conservative by overlooking points of singularity.
AI-generated content may contain errors. Please verify critical information