A \ (B ∪ C) is equivalent to: (A \ B denotes A - B) a) (A \ B) ∪ (A \ C) b) A \ B \ C c) (A \ B) ∩ (A \ C) d) A \ (B ∩ C)

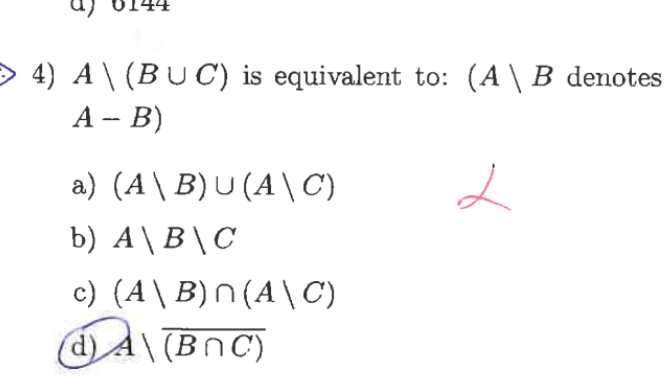
Understand the Problem

The question is asking to determine which expression is equivalent to the set operation A \ (B ∪ C), where \ A \ B denotes A minus B. This involves understanding set theory and operations on sets.

Answer

The equivalent expression is $ (A \setminus B) \cap (A \setminus C) $.

Steps to Solve

Understanding Set Differences and Unions

Starting from the expression ( A \setminus (B \cup C) ), we need to apply the definition of set difference. The set difference ( A \setminus B ) consists of elements in ( A ) that are not in ( B ).

Applying De Morgan's Law

We can rewrite the expression ( A \setminus (B \cup C) ) using De Morgan’s law, which tells us that:

$$ A \setminus (B \cup C) = A \cap (U \setminus (B \cup C)) $$

This means we need to find elements in ( A ) that are not in the union of ( B ) and ( C ).

Using Set Identity

Using the properties of sets, we can express the complement of a union as the intersection of the complements:

$$ U \setminus (B \cup C) = (U \setminus B) \cap (U \setminus C) $$

Thus, we can now say:

$$ A \setminus (B \cup C) = A \cap ((U \setminus B) \cap (U \setminus C)) = A \cap U \setminus B \cap U \setminus C $$

Rewriting the Expression

From this, it follows that:

$$ A \setminus (B \cup C) = A \cap (U \setminus B) \cap (U \setminus C) = A \setminus B \cap A \setminus C $$

Final Simplification

Thus, we can write:

$$ A \setminus (B \cup C) = A \setminus B \cap A \setminus C $$

This leads us to recognize that the correct equivalent expression is:

$$ A \setminus (B \cup C) = (A \setminus B) \cap (A \setminus C) $$

The equivalent expression is ( (A \setminus B) \cap (A \setminus C) ).

More Information

When two sets are combined using the union operation and then we want to find the difference with another set, we can often utilize the distributive properties of set operations. The key takeaway is understanding how to manipulate and simplify set expressions using the laws of set theory.

Tips

Misunderstanding the union and intersection, which may lead to incorrect identifications of equivalent sets.
Forgetting that ( A \setminus (B \cup C) ) signifies all the elements in ( A ) that are not in either ( B ) or ( C ).
Confusing the operations with arithmetic operations, which can lead to overlooking the properties specific to sets.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!