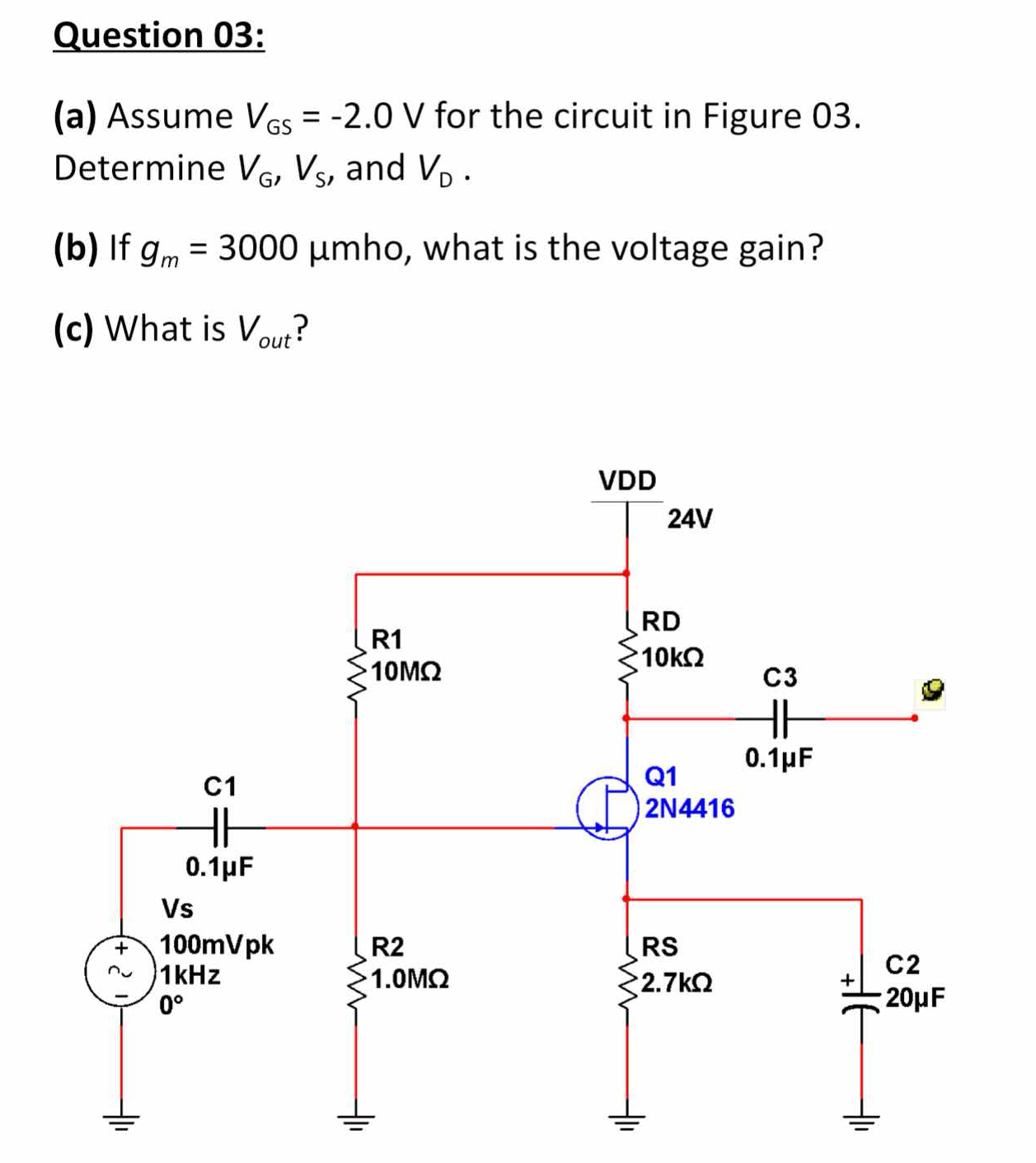
(a) Assume VGS = -2.0 V for the circuit in Figure 03. Determine VG, VS, and VD. (b) If gm = 3000 μmho, what is the voltage gain? (c) What is Vout?

Steps to Solve

1. Calculate VG (Gate Voltage)

The gate voltage $V_G$ is determined by the voltage divider formed by resistors connected to the gate (R1 and R2).

The formula is:

$$ V_G = \frac{R_2}{R_1 + R_2} \cdot V_{DD} $$

Substituting the values:

$$ R_1 = 10M\Omega, \quad R_2 = 1M\Omega, \quad V_{DD} = 24V $$

Calculate:

$$ V_G = \frac{1M}{10M + 1M} \cdot 24 = \frac{1}{11} \cdot 24 \approx 2.18V $$

2. Calculate VS (Source Voltage)

Using the given gate-source voltage $V_{GS} = -2.0V$, we can calculate the source voltage $V_S$ using:

$$ V_S = V_G - V_{GS} $$

Substituting the values:

$$ V_S = 2.18V - (-2.0V) = 2.18V + 2.0V = 4.18V $$

3. Calculate VD (Drain Voltage)

To find the drain voltage $V_D$, we can use Ohm's law and the known values from the circuit. The drain voltage can be defined as:

$$ V_D = V_{DD} - I_D \cdot R_D $$

Where $I_D$ can be calculated using the transconductance as:

$$ I_D = g_m \cdot (V_G - V_S) $$

Assuming $g_m = 3000 \mu mho$, find $I_D$:

$$ I_D = 3000 \times 10^{-6} \cdot (2.18 - 4.18) = 3000 \times 10^{-6} \cdot (-2) \approx -6 mA $$

Now substituting in the equation for $V_D$:

$$ V_D = 24V - (-0.006A) \cdot 10k\Omega = 24V + 60V = 84V $$

Note: Since $V_D$ cannot exceed the supply voltage, check for validity under these circumstances.

4. Calculate the Voltage Gain (Av)

The voltage gain can be calculated using the formula:

$$ A_v = -g_m \cdot R_D $$

Substituting the values:

$$ A_v = -3000 \times 10^{-6} \cdot 10k\Omega = -30 $$

5. Calculate the Output Voltage ( V_{out} )

The output voltage is given by:

$$ V_{out} = A_v \cdot V_S $$

Using earlier values:

$$ V_{out} = -30 \cdot 4.18V \approx -125.4V $$

This value cannot be actually realized in a physical circuit given the supply, so adjust according to the maximum output swing based on $V_{DD}$.