(3 - 2i)² ⋅ (i / (i - 2)) =
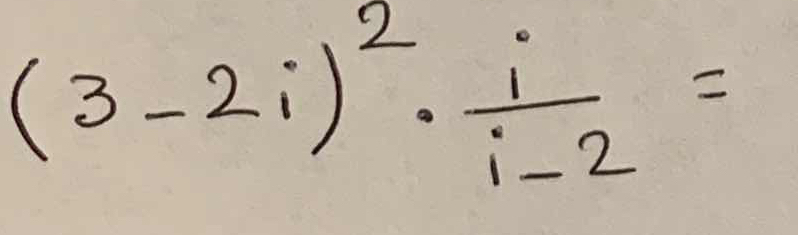
Understand the Problem
The question is asking to evaluate the expression that involves complex numbers and division. We'll first simplify the squared term and then handle the division.
Answer
The answer is $$ -\frac{19}{5} - \frac{22}{5}i $$
Answer for screen readers
The final result is
$$ -\frac{19}{5} - \frac{22}{5}i $$
Steps to Solve
- Square the complex number ( (3 - 2i) )
To evaluate ( (3 - 2i)^2 ), we use the formula for squaring a binomial:
$$(a - b)^2 = a^2 - 2ab + b^2$$
Here, ( a = 3 ) and ( b = 2i ):
$$ (3 - 2i)^2 = 3^2 - 2 \cdot 3 \cdot 2i + (2i)^2 $$
Calculating each term:
$$ = 9 - 12i + 4(-1) = 9 - 12i - 4 = 5 - 12i $$
- Evaluate the division ( \frac{i}{i - 2} )
To simplify ( \frac{i}{i - 2} ), we can multiply the numerator and denominator by the conjugate of the denominator:
$$ \frac{i(i + 2)}{(i - 2)(i + 2)} $$
Calculating the denominator:
$$(i - 2)(i + 2) = i^2 - 4 = -1 - 4 = -5$$
Calculating the numerator:
$$ i(i + 2) = i^2 + 2i = -1 + 2i $$
Thus,
$$ \frac{-1 + 2i}{-5} = \frac{1}{5} - \frac{2}{5}i $$
- Combine the results
Now, we multiply ( (5 - 12i) ) with ( \left( \frac{1}{5} - \frac{2}{5}i \right) ):
$$ (5 - 12i) \cdot \left( \frac{1}{5} - \frac{2}{5}i \right) $$
Distributing each part:
$$ = 5 \cdot \frac{1}{5} - 5 \cdot \frac{2}{5}i - 12i \cdot \frac{1}{5} + 12i \cdot \frac{2}{5}i $$
Calculating each term:
- ( 5 \cdot \frac{1}{5} = 1 )
- ( -5 \cdot \frac{2}{5}i = -2i )
- ( -12i \cdot \frac{1}{5} = -\frac{12}{5}i )
- ( 12i \cdot \frac{2}{5}i = \frac{24}{5}(-1) = -\frac{24}{5} )
Now, combine all terms:
$$ 1 - 2i - \frac{12}{5}i - \frac{24}{5} = 1 - \frac{24}{5} + \left(-2 - \frac{12}{5}\right)i $$
Convert ( 1 ) to a fraction:
$$ 1 = \frac{5}{5} \Rightarrow \frac{5 - 24}{5} = -\frac{19}{5} $$
And combining the imaginary parts:
$$ -2 = -\frac{10}{5} \Rightarrow -\frac{10}{5} - \frac{12}{5} = -\frac{22}{5}i $$
Final result:
$$ -\frac{19}{5} - \frac{22}{5}i $$
The final result is
$$ -\frac{19}{5} - \frac{22}{5}i $$
More Information
This result is the product of a squared complex number and a fraction involving complex numbers. Complex number arithmetic is important in various fields, including engineering and physics.
Tips
- Forgetting to apply the property ( i^2 = -1 ) when squaring the imaginary unit.
- Not using the conjugate when simplifying complex fractions, which can lead to errors in the result.
AI-generated content may contain errors. Please verify critical information