∫ -5cos(πx) dx
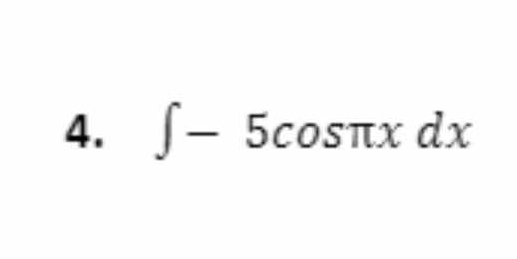
Understand the Problem
The question is asking us to find the integral of the function -5cos(πx) with respect to x. This requires knowledge of integration techniques to solve the problem.
Answer
$$ -\frac{5}{\pi} \sin(\pi x) + C $$
Answer for screen readers
The final answer is: $$ -\frac{5}{\pi} \sin(\pi x) + C $$
Steps to Solve
- Set Up the Integral
We begin with the integral we need to solve: $$ \int -5\cos(\pi x) , dx $$
- Factor Out the Constant
We can factor the constant (-5) out of the integral: $$ -5 \int \cos(\pi x) , dx $$
- Integrate Cosine Function
The integral of $\cos(kx)$ is $\frac{1}{k} \sin(kx) + C$. Here, $k = \pi$: $$ -5 \cdot \frac{1}{\pi} \sin(\pi x) + C $$
- Simplify the Expression
Now simplify this expression: $$ -\frac{5}{\pi} \sin(\pi x) + C $$
The final answer is: $$ -\frac{5}{\pi} \sin(\pi x) + C $$
More Information
This integral is a common example in calculus, demonstrating the use of standard integration techniques. The function $\cos(\pi x)$ has a periodic nature, which is reflected in the sine function that results from the integration. The constant $C$ represents the constant of integration.
Tips
- Confusing the integral of cosine with that of sine: Remember that the integral of $\cos(kx)$ leads to $\frac{1}{k} \sin(kx)$.
- Forgetting to include the constant of integration $C$ at the end.