∫ 1/√x dx
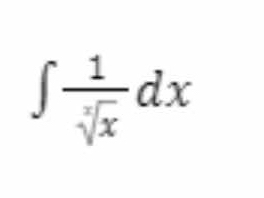
Understand the Problem
The question is asking for the integral of the function 1 over the square root of x with respect to x, which requires performing integration techniques.
Answer
$$ 2\sqrt{x} + C $$
Answer for screen readers
$$ 2\sqrt{x} + C $$
Steps to Solve
- Rewrite the integral in exponent form
The integral can be expressed using exponent notation. We know that $ \sqrt{x} = x^{1/2} $, so we rewrite the integrand as:
$$ \frac{1}{\sqrt{x}} = x^{-1/2} $$
This gives us the integral:
$$ \int x^{-1/2} , dx $$
- Apply the power rule of integration
Using the power rule of integration, which states that:
$$ \int x^n , dx = \frac{x^{n+1}}{n+1} + C $$
for any real number $ n \neq -1 $, we apply it to our integral. Here, $ n = -\frac{1}{2} $:
$$ n + 1 = -\frac{1}{2} + 1 = \frac{1}{2} $$
Now we can evaluate the integral:
$$ \int x^{-1/2} , dx = \frac{x^{1/2}}{1/2} + C = 2x^{1/2} + C $$
- Write the final result
Thus, the integral of the function $ \frac{1}{\sqrt{x}} $ with respect to $ x $ is:
$$ \int \frac{1}{\sqrt{x}} , dx = 2\sqrt{x} + C $$
$$ 2\sqrt{x} + C $$
More Information
The result of this integral shows that the area under the curve of the function $ \frac{1}{\sqrt{x}} $ with respect to $ x $ grows proportionally to $ \sqrt{x} $. This has applications in various fields such as physics, particularly in problems involving rates of change.
Tips
- Forgetting to add the constant of integration, $ C $.
- Misapplying the power rule, especially with negative exponents.