∫ -5cos(πx) dx
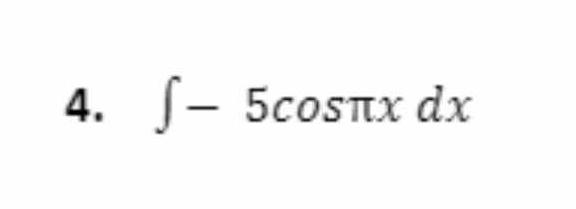
Understand the Problem
The question is asking for the indefinite integral of the function -5cos(πx) with respect to x. This involves applying standard integration techniques to find the antiderivative.
Answer
The integral is $-\frac{5}{\pi} \sin(\pi x) + C$.
Answer for screen readers
The indefinite integral is: $$ -\frac{5}{\pi} \sin(\pi x) + C $$
Steps to Solve
-
Identify the Integral Form We need to integrate the function $-5 \cos(\pi x)$. The general integral of $\cos(kx)$ is known to be $\frac{1}{k} \sin(kx) + C$, where $C$ is the constant of integration.
-
Determine the Constant k In our case, the function is $-5 \cos(\pi x)$, so we identify $k = \pi$.
-
Apply the Integration Formula Using the formula for integration, we substitute $k = \pi$ into the general form: $$ \int -5 \cos(\pi x) , dx = -5 \cdot \frac{1}{\pi} \sin(\pi x) + C $$
-
Simplify the Expression This gives us: $$ -\frac{5}{\pi} \sin(\pi x) + C $$
The indefinite integral is: $$ -\frac{5}{\pi} \sin(\pi x) + C $$
More Information
The integral represents the antiderivative of the function $-5 \cos(\pi x)$. The presence of $\pi$ in the argument of the cosine affects the frequency of the sine function in the resulting antiderivative.
Tips
- Forgetting to include the constant of integration $C$ after finding the indefinite integral.
- Misidentifying the value of $k$ in the integration formula, leading to incorrect results.
AI-generated content may contain errors. Please verify critical information