5^4 x 3a^2 ÷ 6a^-3
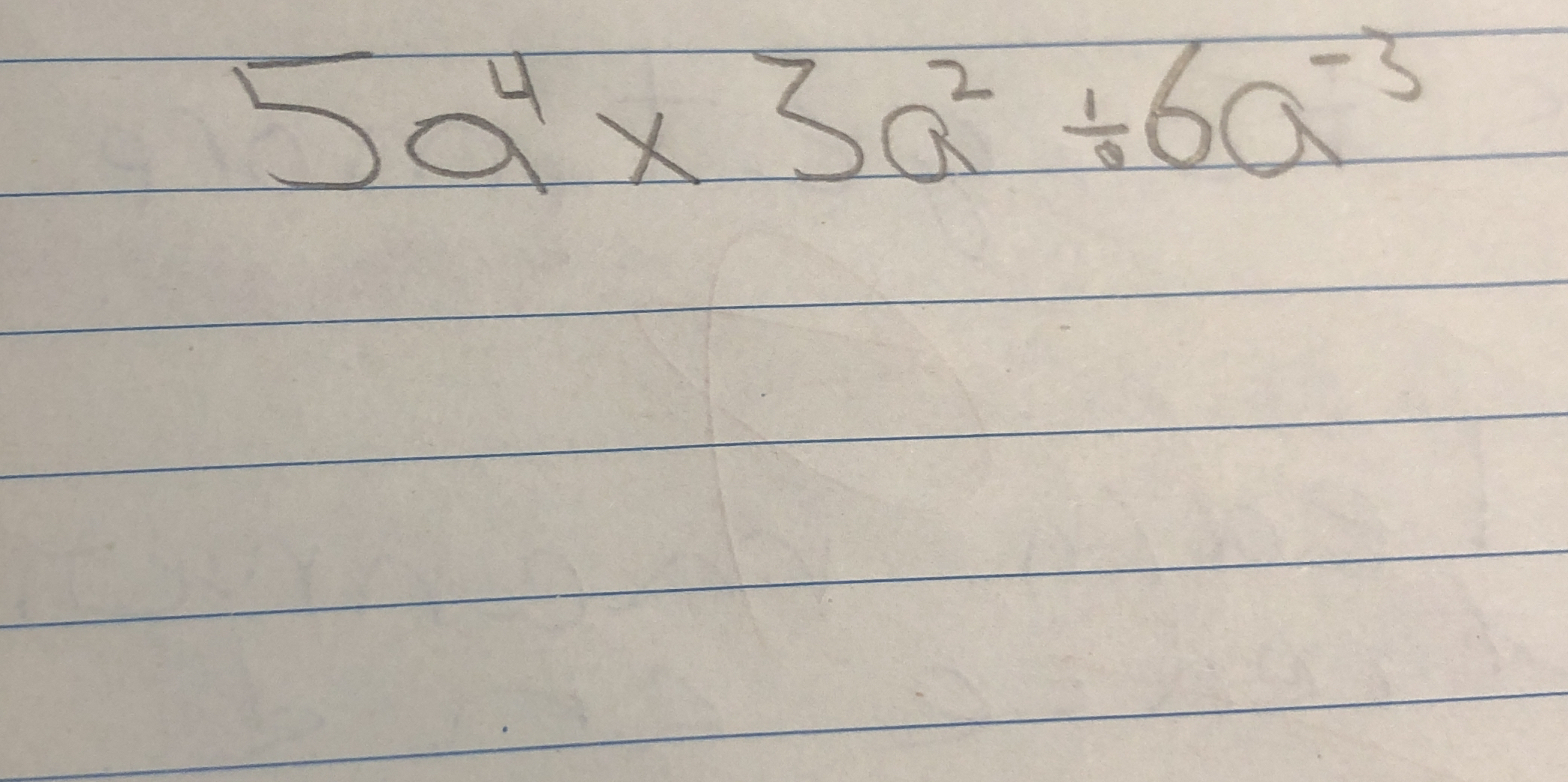
Understand the Problem
The question involves performing operations on algebraic expressions that include exponents. Specifically, it asks for the result of multiplying and dividing the expressions 5^4, 3a^2, and 6a^-3.
Answer
$$ 312.5a^5 $$
Answer for screen readers
The final result is: $$ 312.5a^5 $$
Steps to Solve
-
Calculate $5^4$ First, we find the value of $5^4$.
$$ 5^4 = 5 \times 5 \times 5 \times 5 = 625 $$ -
Combine the terms using multiplication Next, we multiply $625$ with $3a^2$.
$$ 625 \times 3a^2 = 1875a^2 $$ -
Divide the expression by $6a^{-3}$ Now, we divide $1875a^2$ by $6a^{-3}$.
This can be rewritten as:
$$ \frac{1875a^2}{6a^{-3}} $$ -
Simplify the coefficients Divide the numerical coefficients: $$ \frac{1875}{6} = 312.5 $$
-
Combine the variable expressions Next, apply the exponent rules for the variable $a$:
$$ a^2 \div a^{-3} = a^{2 - (-3)} = a^{2 + 3} = a^5 $$ -
Combine the results Finally, bring the simplified coefficient and variable together:
$$ 312.5a^5 $$
The final result is: $$ 312.5a^5 $$
More Information
The expression combines addition and division of exponents and coefficients. This illustrates the power of exponents and the rules of multiplying and dividing algebraic expressions.
Tips
- Confusing the subtraction of exponents when dividing. Remember to subtract the exponent of the denominator from the exponent of the numerator.
- Failing to simplify coefficients properly. Always simplify fractions when possible.
AI-generated content may contain errors. Please verify critical information