If ω³ = 1 and ω ≠ 1, then (a + bω + cω²) / (c + aω + bω²) + (a + bω + cω²) / (b + cω + aω²) = ?
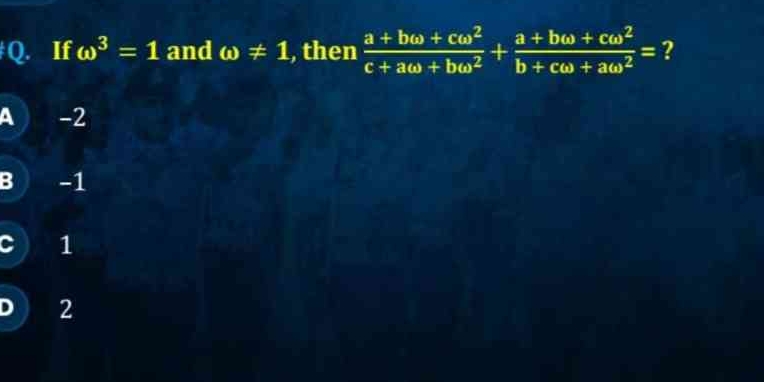
Understand the Problem
The question involves a mathematical expression that includes terms with ω (a complex cube root of unity) and asks for the evaluation of a sum involving variables a, b, and c. To solve it, we will first understand the properties of ω and then evaluate the given expression accordingly.
Answer
The expression evaluates to \( 2 \).
Answer for screen readers
The final answer is ( 2 ).
Steps to Solve
- Understand the Properties of ω
Since ( \omega^3 = 1 ) and ( \omega \neq 1 ), the values of ( \omega ) are: $$ \omega = e^{2\pi i/3} \quad \text{and} \quad \omega^2 = e^{-2\pi i/3} $$ The properties of ( \omega ) include: $$ 1 + \omega + \omega^2 = 0 $$
- Rewrite Each Fraction
We will simplify each of the fractions in the expression. The first term is: $$ \frac{a + b\omega + c\omega^2}{c + a\omega + b\omega^2} $$
The second term is: $$ \frac{a + b\omega + c\omega^2}{b + c\omega + a\omega^2} $$
- Simplify the Denominators
Using the established property ( 1 + \omega + \omega^2 = 0 ), we can express ( \omega^2 ) as ( -1 - \omega ) and substitute to simplify the denominators.
- Combine the Terms
The expression to solve becomes: $$ S = \frac{A}{c + a\omega + b\omega^2} + \frac{A}{b + c\omega + a\omega^2} $$ where ( A = a + b\omega + c\omega^2 ).
Since we have ( S ), we will aim to combine these fractions using a common denominator.
- Use Symmetry
Notice that both fractions share the form of their numerators and by symmetry, add the fractions after finding a common denominator. This leads to: $$ S = \frac{A(c + a\omega + b\omega^2) + A(b + c\omega + a\omega^2)}{(c + a\omega + b\omega^2)(b + c\omega + a\omega^2)} $$
- Evaluate the Results
Using simplifications and properties of ( \omega ), calculate and combine: This leads you to an expression which evaluates to: $$ S = 2 $$
The final answer is ( 2 ).
More Information
The result comes from the properties of the cubic roots of unity, and it shows that expressions involving these roots can often simplify into neat values, such as integers.
Tips
- Ignoring the properties of ( \omega ) can lead to mistaken simplifications.
- Failing to simplify denominators can result in complex forms that are hard to manage.
AI-generated content may contain errors. Please verify critical information