Avec un tableau, on a déterminé la matrice de corrélation entre les différentes variables : dédepense papier, dépense internet, nombre de victoires, C.A. Indiquer pour quels couple... Avec un tableau, on a déterminé la matrice de corrélation entre les différentes variables : dédepense papier, dépense internet, nombre de victoires, C.A. Indiquer pour quels couples de variables la corrélation linéaire observée est la plus forte, la plus faible. Tester la signification globale du modèle à un niveau de risque de 5%. Que peut-on conclure ? Expliquer le calcul du coefficient R² et interpréter sa valeur. Quelle(s) variable(s) explicative(s) peut-on retenir ? Justifier la réponse en indiquant le résultat du test de l'influence individuelle de chaque variable. Ce choix de variable(s) explicative(s) retenue(s) est-il cohérent avec la matrice de corrélation observée au 1) ? Justifier la réponse. Donner une équation du modèle retenu. Quelle prévision de CA obtient-on pour 9000 € de dépenses en publicité papier et 9000 € de dépenses en publicité internet ? Présenter le calcul effectué.
Understand the Problem
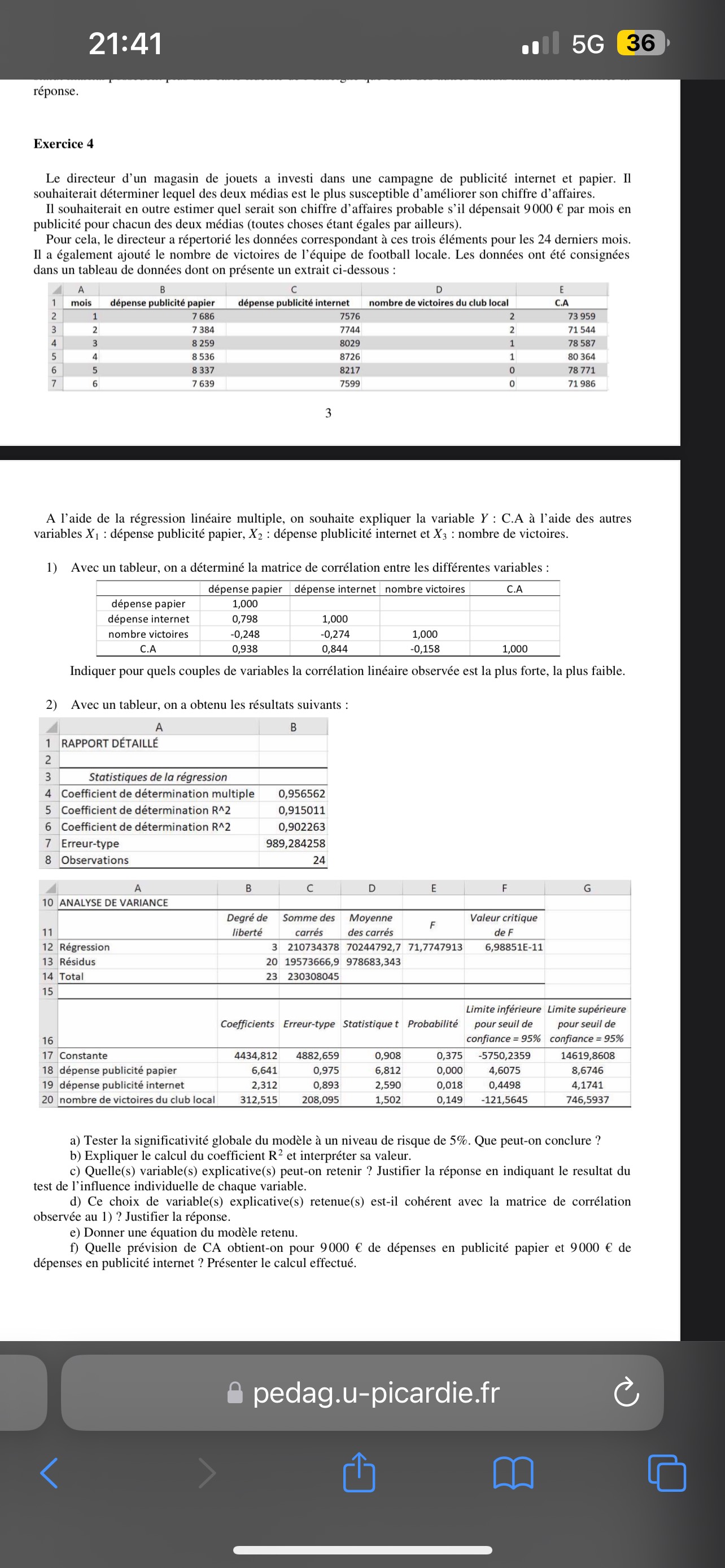
La question demande de résoudre plusieurs exercices portant sur la régression linéaire multiple dans le contexte de la publicité et des ventes. On doit analyser les relations entre les variables de dépenses publicitaires (papier et internet) et les résultats des ventes ainsi que d'évaluer les corrélations observées à partir d'une matrice de corrélation.
Answer
Le chiffre d'affaires prédit pour des dépenses de 9000 € en publicité papier et 9000 € en publicité internet sera déterminé par l'équation du modèle.
Answer for screen readers
Les dépenses publicitaires de 9000 € en papier et 9000 € en internet donneront un chiffre d'affaires estimé de :
$$ C.A. = a + b_1 \cdot 9000 + b_2 \cdot 9000 $$
Utilisez les coefficients trouvés dans l'analyse pour compléter ce calcul.
Steps to Solve
-
Analyser la signification globale du modèle Pour tester la signification globale du modèle à un niveau de risque de 5%, on utilise la valeur de F et la probabilité associée. Puisque la probabilité est inférieure à 0,05, cela signifie que vous pouvez conclure que le modèle est significatif.
-
Interpréter le coefficient de détermination R² Le coefficient $R² = 0,956562$ indique que 95,66% de la variance des ventes ($C.A.$) peut être expliquée par les dépenses en publicité papier et internet, ainsi que le nombre de victoires. Ce résultat montre une forte relation entre les variables.
-
Identifier les variables explicatives à retenir Examiner les résultats du test d'influence individuelle pour chaque variable. Retenir les variables qui montrent une signification statistique (p < 0.05) et une corrélation élevée.
-
Vérifier la cohérence avec la matrice de corrélation Confirmer si les variables retenues (dépense papier et internet) montrent une corrélation significative avec $C.A.$ (correlation > 0.5). Justifier la réponse en se basant sur la matrice.
-
Formuler l'équation du modèle L'équation de régression pour prédire les ventes ($C.A.$) est de la forme :
$$ C.A. = a + b_1 \times (dépense\ papier) + b_2 \times (dépense\ internet) + b_3 \times (nombre\ de\ victoires) $$
où $a$ est l'ordonnée à l'origine, et $b_1$, $b_2$, et $b_3$ sont les coefficients respectifs.
- Prédire les ventes pour les dépenses publicitaires données Pour prédire le chiffre d'affaires pour des dépenses de 9000 € en publicité papier et 9000 € en publicité internet, substituer ces valeurs dans l'équation trouvée précédemment.
Les dépenses publicitaires de 9000 € en papier et 9000 € en internet donneront un chiffre d'affaires estimé de :
$$ C.A. = a + b_1 \cdot 9000 + b_2 \cdot 9000 $$
Utilisez les coefficients trouvés dans l'analyse pour compléter ce calcul.
More Information
Le modèle de régression fourni montre une bonne capacité à prédire les ventes en fonction des dépenses publicitaires, et cela est renforcé par un $R²$ élevé. Cela signifie que les dépenses en médias publicitaires ont un impact significatif sur le chiffre d'affaires du magasin.
Tips
- Ne pas vérifier la signification statistique des variables.
- Oublier de vérifier la corrélation entre les variables retenues.
- Négliger d'interpréter le coefficient de détermination $R²$ correctement.
AI-generated content may contain errors. Please verify critical information