3/(x^2 - 4) + 1/((x - 2)^2)
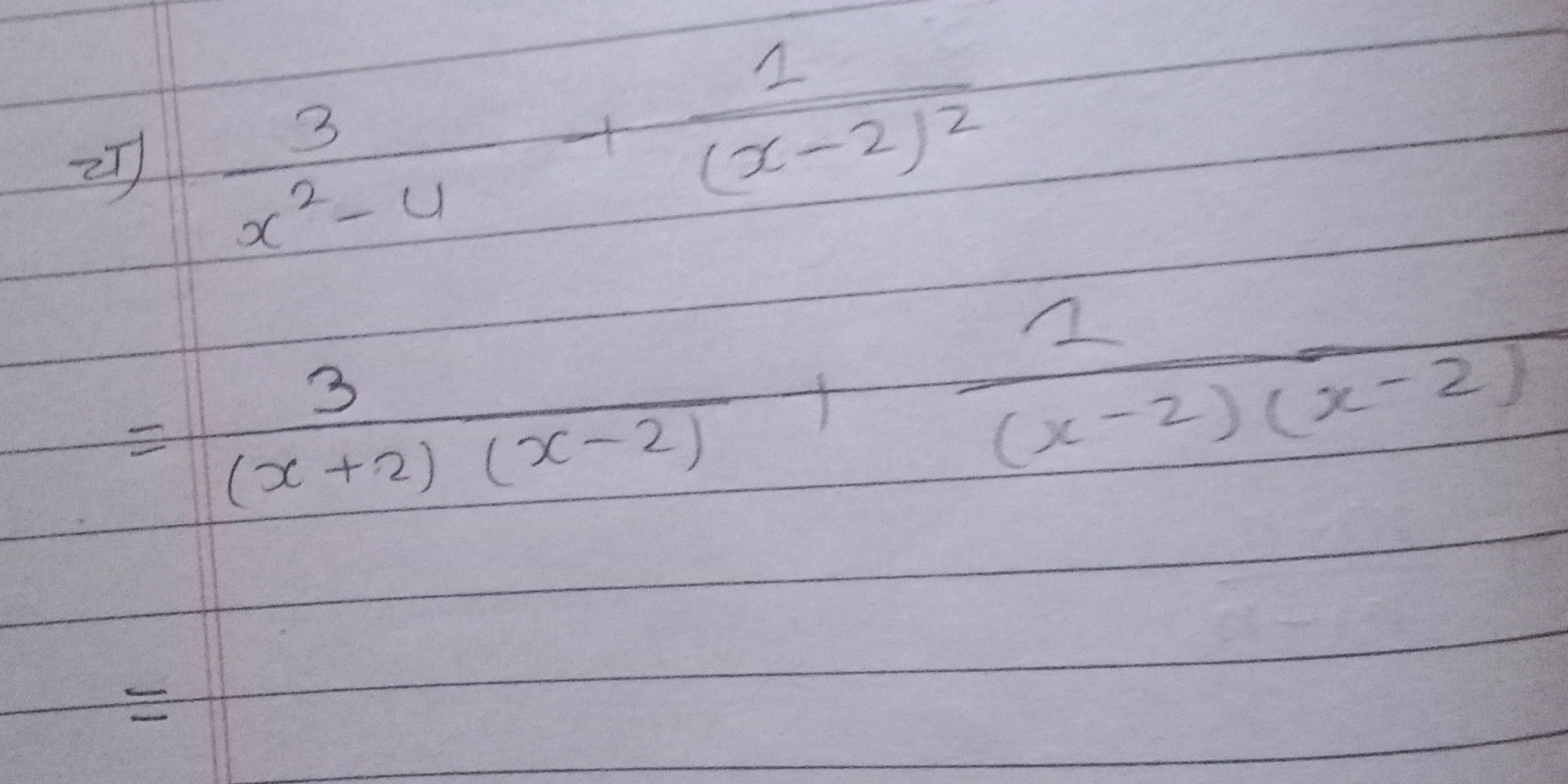
Understand the Problem
The question appears to involve algebraic manipulation, specifically adding fractions with polynomials as denominators. The goal is likely to simplify the expression or perform some operation on it.
Answer
The simplified expression is $\frac{4(x - 1)}{(x - 2)^2(x + 2)}$.
Answer for screen readers
The final simplified expression is: $$ \frac{4(x - 1)}{(x - 2)^2(x + 2)} $$
Steps to Solve
- Identify the Denominators
The denominators in the expression are $x^2 - 4$ and $(x - 2)^2$.
- Factor the Denominator
The first denominator can be factored: $$ x^2 - 4 = (x - 2)(x + 2) $$ So the expression now looks like: $$ \frac{3}{(x - 2)(x + 2)} + \frac{1}{(x - 2)^2} $$
- Find the Common Denominator
The least common denominator (LCD) is: $$ (x - 2)^2(x + 2) $$
- Rewrite Each Fraction with the LCD
Multiply each fraction to get the common denominator:
-
The first fraction: $$ \frac{3}{(x - 2)(x + 2)} \cdot \frac{(x - 2)}{(x - 2)} = \frac{3(x - 2)}{(x - 2)^2(x + 2)} $$
-
The second fraction: $$ \frac{1}{(x - 2)^2} \cdot \frac{(x + 2)}{(x + 2)} = \frac{(x + 2)}{(x - 2)^2(x + 2)} $$
- Combine the Numerators
Now add the two fractions: $$ \frac{3(x - 2) + (x + 2)}{(x - 2)^2(x + 2)} $$
- Simplify the Numerator
Expand the numerator: $$ 3(x - 2) + (x + 2) = 3x - 6 + x + 2 = 4x - 4 $$
- Final Expression
Combine the simplified numerator with the denominator: $$ \frac{4(x - 1)}{(x - 2)^2(x + 2)} $$
The final simplified expression is: $$ \frac{4(x - 1)}{(x - 2)^2(x + 2)} $$
More Information
This expression represents the combined result of the two fractions. Factoring and finding a common denominator are key steps in this process, making it easier to add rational expressions.
Tips
- Forgetting to factor the denominators properly.
- Not finding a common denominator.
- Failing to simplify the numerator after combining the fractions.
AI-generated content may contain errors. Please verify critical information