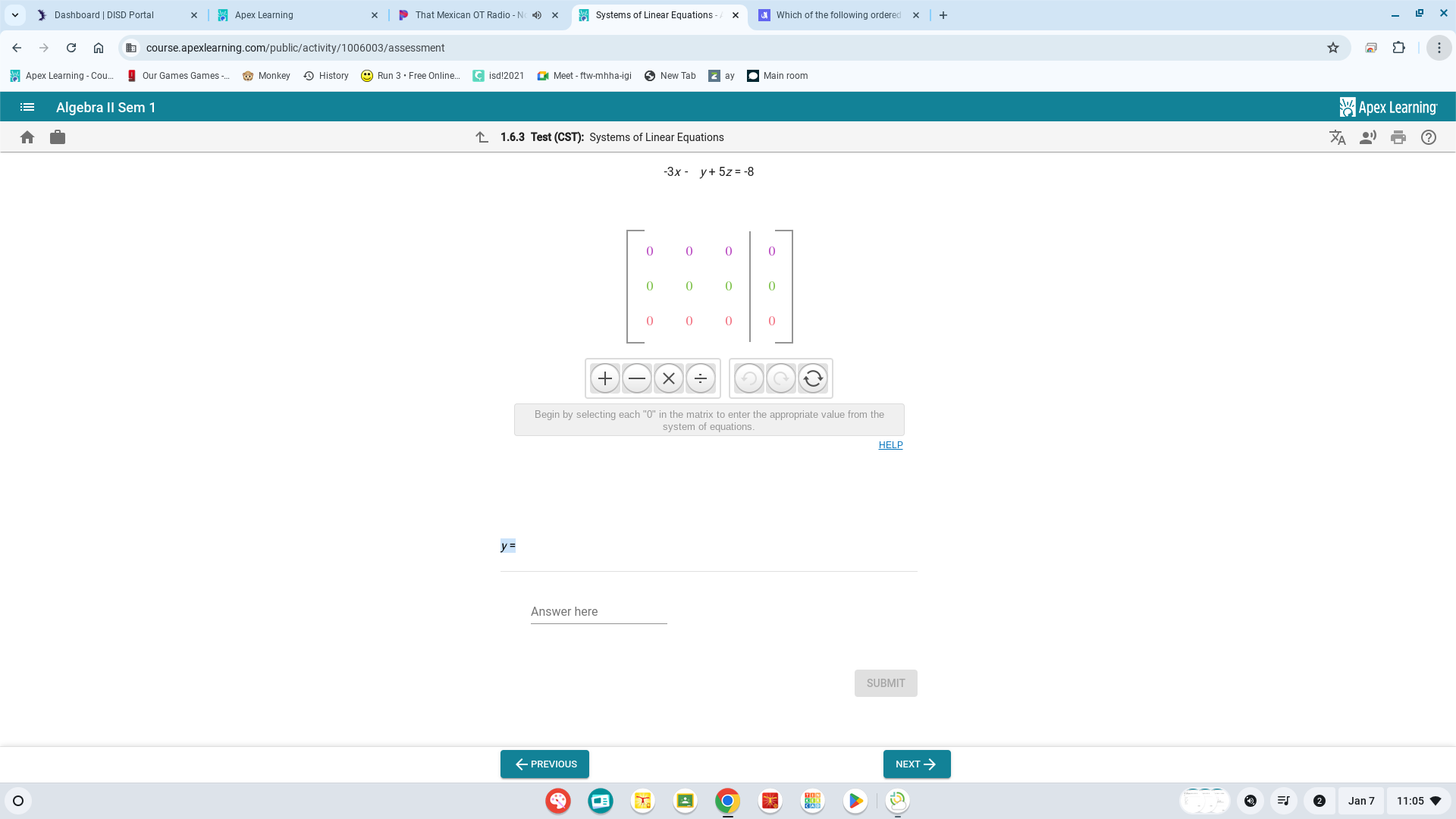
-3x + y + 5z = -8. Fill in the matrix with the correct values.
Understand the Problem
The question presents a system of linear equations involving variables x, y, and z, specifically given as -3x + y + 5z = -8. The user is required to fill in a matrix with appropriate values derived from the given equation.
Answer
The augmented matrix is: $$ \begin{bmatrix} -3 & 1 & 5 & | & -8 \end{bmatrix} $$
Answer for screen readers
The augmented matrix for the equation is: $$ \begin{bmatrix} -3 & 1 & 5 & | & -8 \end{bmatrix} $$
Steps to Solve
- Identifying the Coefficients and Constant From the equation given, we identify the coefficients for $x$, $y$, and $z$, as well as the constant term. The equation is: $$ -3x + 1y + 5z = -8 $$ So, the coefficients are:
- For $x$: $-3$
- For $y$: $1$
- For $z$: $5$
- Constant term: $-8$
-
Setting Up the Augmented Matrix We create an augmented matrix using the coefficients of the variables and the constant term. The matrix will have the form: $$ \begin{bmatrix} -3 & 1 & 5 & | & -8 \end{bmatrix} $$ This matrix consists of the coefficients placed in the first three columns and the constant term in the last column.
-
Finalizing the Matrix Now we can fill in the matrix by entering the identified values in their respective positions: $$ \begin{bmatrix} -3 & 1 & 5 & | & -8 \end{bmatrix} $$ Since this is a single equation, there’s no need for additional rows.
The augmented matrix for the equation is: $$ \begin{bmatrix} -3 & 1 & 5 & | & -8 \end{bmatrix} $$
More Information
An augmented matrix is a convenient way to represent a system of linear equations. Each row corresponds to a linear equation, with coefficients organized consecutively, followed by the constant term.
Tips
- Not including the constant term: Ensure you always add the constant term to the last column of your matrix.
- Misidentifying coefficients: Double-check that you're looking at the correct terms from the equation, especially the signs.
AI-generated content may contain errors. Please verify critical information