-x1 + 2x2 - 2x3 = -3; x1 - x2 + x3 = 2; x1 + x2 - 3x3 = -6
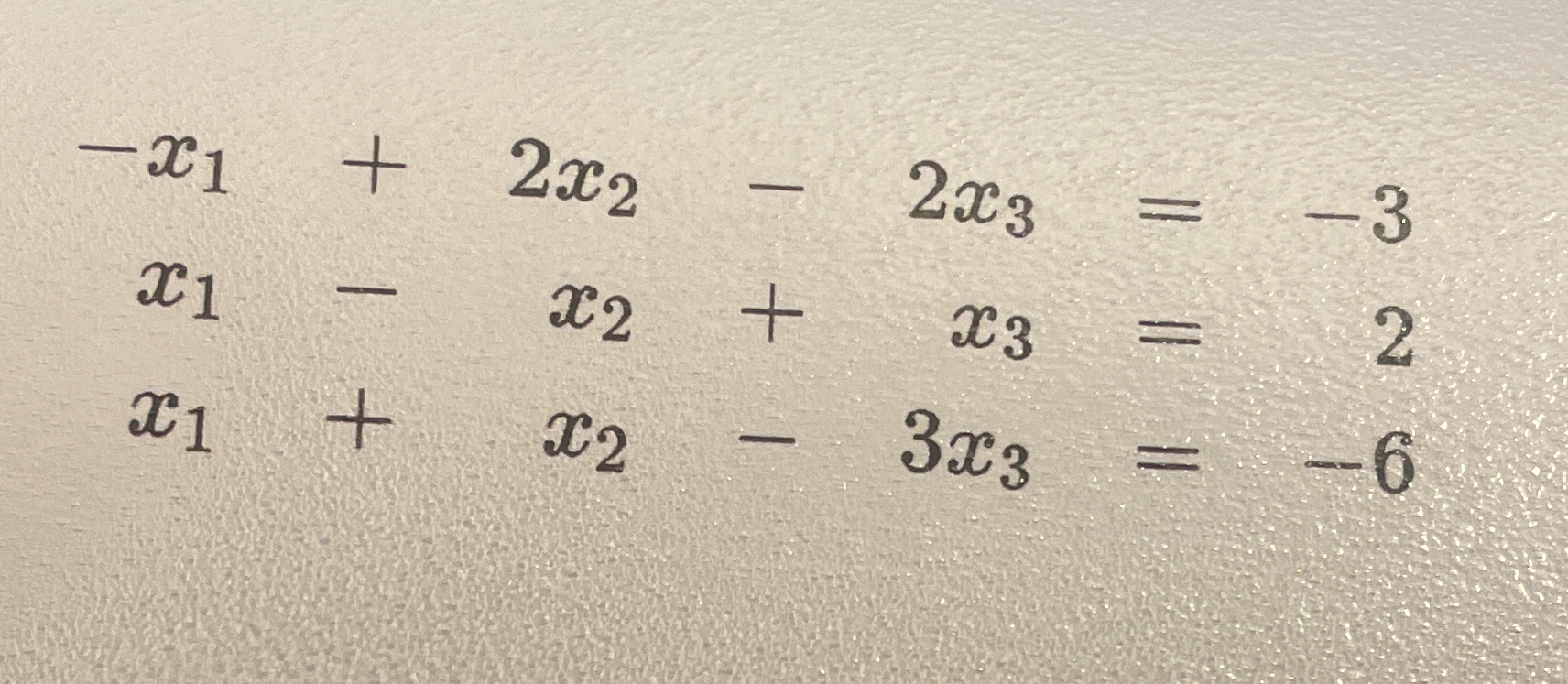
Understand the Problem
The question presents a system of linear equations that needs to be solved. Each equation contains variables x1, x2, and x3, which we need to find. This is a common problem in algebra.
Answer
The solution is $x_1 = 1$, $x_2 = 2$, $x_3 = 3$.
Answer for screen readers
The solution to the system of equations is:
$$
x_1 = 1, \quad x_2 = 2, \quad x_3 = 3
$$
Steps to Solve
-
Write down the equations
The given system of equations is:
$$
-x_1 + 2x_2 - 2x_3 = -3 \quad (1)
$$
$$
x_1 - x_2 + x_3 = 2 \quad (2)
$$
$$
x_1 + x_2 - 3x_3 = -6 \quad (3)
$$ -
Isolate one variable
Start with equation (2) to isolate $x_1$:
$$
x_1 = x_2 - x_3 + 2 \quad (4)
$$ -
Substitute into other equations
Substitute equation (4) into equations (1) and (3):
For equation (1):
$$
-(x_2 - x_3 + 2) + 2x_2 - 2x_3 = -3
$$
Simplifying gives:
$$
-x_2 + x_3 - 2 + 2x_2 - 2x_3 = -3
$$
Combine like terms:
$$
x_2 - x_3 - 2 = -3
$$
This simplifies to:
$$
x_2 - x_3 = -1 \quad (5)
$$
For equation (3):
$$
(x_2 - x_3 + 2) + x_2 - 3x_3 = -6
$$
Simplifying gives:
$$
x_2 - x_3 + 2 + x_2 - 3x_3 = -6
$$
This simplifies to:
$$
2x_2 - 4x_3 + 2 = -6
$$
Removing 2 from both sides:
$$
2x_2 - 4x_3 = -8
$$
Dividing by 2 gives:
$$
x_2 - 2x_3 = -4 \quad (6)
$$
-
Solve the new equations
You now have two equations, (5) and (6):
From (5):
$$
x_2 = x_3 - 1 \quad (7)
$$
Substitute (7) into (6):
$$
(x_3 - 1) - 2x_3 = -4
$$
This simplifies to:
$$
-x_3 - 1 = -4
$$
So:
$$
-x_3 = -3 \quad \Rightarrow x_3 = 3
$$
-
Find remaining variables
Substituting $x_3 = 3$ back into (7):
$$
x_2 = 3 - 1 = 2
$$
Finally, substitute $x_2$ and $x_3$ back into (4) to find $x_1$:
$$
x_1 = 2 - 3 + 2 = 1
$$
-
Final solution
The solution is:
$$
x_1 = 1, \quad x_2 = 2, \quad x_3 = 3
$$
The solution to the system of equations is:
$$
x_1 = 1, \quad x_2 = 2, \quad x_3 = 3
$$
More Information
This solution shows how to solve a system of linear equations using substitution and simplification. Each step builds on the previous to find the values of the variables systematically.
Tips
- Forgetting to substitute correctly can lead to errors. Always double-check the equations after substitution.
- Neglecting to simplify fully can result in incorrect equations. Make sure to combine like terms.
AI-generated content may contain errors. Please verify critical information