∫ 1/√x dx
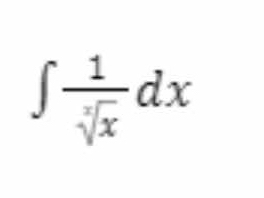
Understand the Problem
The question is asking us to solve the integral of 1 divided by the square root of x with respect to x. This requires applying integration techniques to find the antiderivative.
Answer
The integral evaluates to \( 2\sqrt{x} + C \).
Answer for screen readers
The result of the integral is $$ 2\sqrt{x} + C $$
Steps to Solve
-
Rewrite the Integral We start by rewriting the integrand in a more manageable form. $$ \int \frac{1}{\sqrt{x}} , dx = \int x^{-1/2} , dx $$
-
Apply the Power Rule for Integration Using the power rule for integration, which states that $$ \int x^n , dx = \frac{x^{n+1}}{n+1} + C $$ where ( n \neq -1 ), we can apply it here with ( n = -\frac{1}{2} ). $$ \int x^{-1/2} , dx = \frac{x^{-1/2 + 1}}{-1/2 + 1} + C $$
-
Simplify the Expression Now we simplify the exponents: $$ = \frac{x^{1/2}}{1/2} + C = 2x^{1/2} + C $$
-
Rewrite in Radical Form Finally, we can express the result in a more familiar form using the square root: $$ = 2\sqrt{x} + C $$
The result of the integral is $$ 2\sqrt{x} + C $$
More Information
The integral of ( \frac{1}{\sqrt{x}} ) is a basic integral often encountered in calculus. This integral demonstrates the application of the power rule for integration, which provides a straightforward method to find antiderivatives.
Tips
- Forgetting the Constant of Integration: Always remember to include ( C ) in your final answer after integration.
- Incorrectly Applying the Power Rule: Ensure that the exponent is adjusted correctly; ( n + 1 ) should be calculated accurately.
AI-generated content may contain errors. Please verify critical information