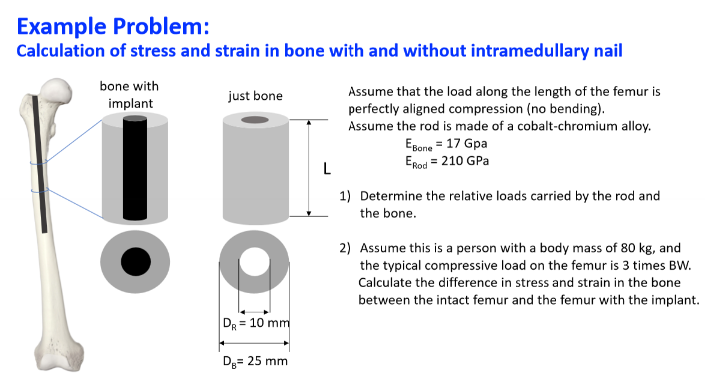
1) Determine the relative loads carried by the rod and the bone. 2) Assume this is a person with a body mass of 80 kg, and the typical compressive load on the femur is 3 times BW.... 1) Determine the relative loads carried by the rod and the bone. 2) Assume this is a person with a body mass of 80 kg, and the typical compressive load on the femur is 3 times BW. Calculate the difference in stress and strain in the bone between the intact femur and the femur with the implant.
Understand the Problem
The question is asking to calculate the relative loads carried by a rod implanted in a femur and the surrounding bone, as well as the difference in stress and strain between an intact femur and a femur with an implant. This involves applying knowledge of material properties and stress-strain relationships in engineering mechanics.
Answer
Load carried by the rod and bone, stress and strain can be calculated using the relations defined for forces, areas, and material properties.
Answer for screen readers
- Load carried by the rod ( F_{rod} ) and bone ( F_{bone} ).
- Stress in the rod ( \sigma_{rod} ) and bone ( \sigma_{bone} ).
- Strain in the rod ( \epsilon_{rod} ) and bone ( \epsilon_{bone} ).
Steps to Solve
- Determine the Area of Rod and Bone To find the loads carried by the rod and bone, first calculate their cross-sectional areas.
The area of the rod ( A_{rod} ) is given by: $$ A_{rod} = \pi \left( \frac{D_R}{2} \right)^2 = \pi \left( \frac{10}{2} \right)^2 = \pi (5^2) = 25\pi , \text{mm}^2 $$
The area of the bone ( A_{bone} ) is given by: $$ A_{bone} = \pi \left( \frac{D_B}{2} \right)^2 = \pi \left( \frac{25}{2} \right)^2 = \pi (12.5^2) = 156.25\pi , \text{mm}^2 $$
-
Calculate Total Load Calculate the total load ( F_{total} ) on the femur. Given a body mass of 80 kg and using the typical compressive load of 3 times body weight (BW): $$ F_{total} = 3 \times (80 , \text{kg} \times 9.81 , \text{m/s}^2) = 3 \times 784.8 , \text{N} = 2354.4 , \text{N} $$
-
Calculate Load Carried by Rod and Bone Using the area ratios to determine the proportion of the load carried by the rod and the bone: Let ( F_{rod} ) be the load carried by the rod and ( F_{bone} ) be the load carried by the bone.
Total area: $$ A_{total} = A_{rod} + A_{bone} = 25\pi + 156.25\pi = 181.25\pi , \text{mm}^2 $$
Thus, the loads can be calculated as: $$ F_{rod} = F_{total} \cdot \frac{A_{rod}}{A_{total}} $$
$$ F_{bone} = F_{total} \cdot \frac{A_{bone}}{A_{total}} $$
- Calculate Stress Stress ( \sigma ) can be found using the formula: $$ \sigma = \frac{F}{A} $$
Stress in the rod ( \sigma_{rod} ): $$ \sigma_{rod} = \frac{F_{rod}}{A_{rod}} $$
Stress in the bone ( \sigma_{bone} ): $$ \sigma_{bone} = \frac{F_{bone}}{A_{bone}} $$
- Calculate Strain Strain ( \epsilon ) can be calculated using the formula: $$ \epsilon = \frac{\sigma}{E} $$
Thus, Strain in rod ( \epsilon_{rod} ): $$ \epsilon_{rod} = \frac{\sigma_{rod}}{E_{rod}} $$
Strain in bone ( \epsilon_{bone} ): $$ \epsilon_{bone} = \frac{\sigma_{bone}}{E_{bone}} $$
- Load carried by the rod ( F_{rod} ) and bone ( F_{bone} ).
- Stress in the rod ( \sigma_{rod} ) and bone ( \sigma_{bone} ).
- Strain in the rod ( \epsilon_{rod} ) and bone ( \epsilon_{bone} ).
More Information
This problem involves using principles of mechanics and materials to determine how loads are distributed in a bone and an implant. The calculations help understand the implications of using implants in medical applications.
Tips
- Forgetting to convert units (e.g., mm² to m²) when using SI units for forces.
- Miscalculating the areas of the rod and bone.
- Confusing stress and strain calculations, especially the use of Young's modulus.
AI-generated content may contain errors. Please verify critical information