Find (f + g)(f - g)(f g)(f/g) for i) f(x) = 4x + 3, g(x) = 2x - 1 ii) f(x) = 2x^2, g(x) = x + 1.
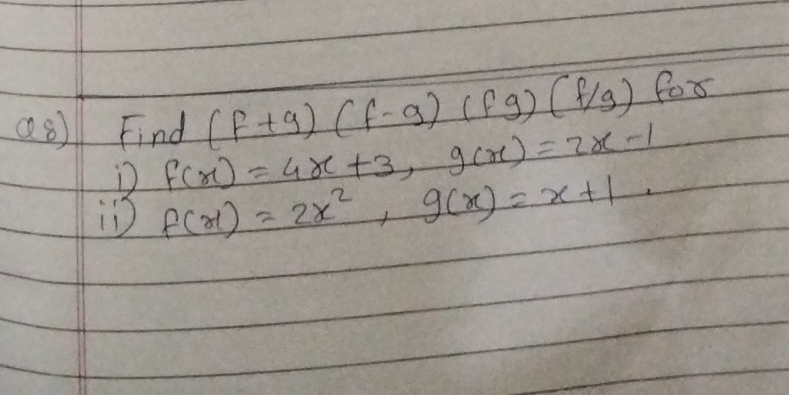
Understand the Problem
The question is asking to find the expression (f + g)(f - g)(f g)(f/g) for the given functions f(x) and g(x) provided in both parts i and ii. It requires performing algebraic operations on the functions to arrive at the final expression.
Answer
For part i: $$ (6x + 2)(2x + 4)(8x^2 + 2x - 3)\left(\frac{4x + 3}{2x - 1}\right) $$ For part ii: $$ (2x^2 + x + 1)(2x^2 - x - 1)(2x^3 + 2x^2)\left(\frac{2x^2}{x + 1}\right) $$
Answer for screen readers
For part i:
$$ (f + g)(f - g)(f \cdot g)(\frac{f}{g}) = (6x + 2)(2x + 4)(8x^2 + 2x - 3)\left(\frac{4x + 3}{2x - 1}\right) $$
For part ii:
$$ (f + g)(f - g)(f \cdot g)(\frac{f}{g}) = (2x^2 + x + 1)(2x^2 - x - 1)(2x^3 + 2x^2)\left(\frac{2x^2}{x + 1}\right) $$
Steps to Solve
- Evaluate for functions f and g
For part i, we have:
$$ f(x) = 4x + 3 $$
$$ g(x) = 2x - 1 $$
For part ii:
$$ f(x) = 2x^2 $$
$$ g(x) = x + 1 $$
- Calculate ( f + g )
For part i:
$$ f + g = (4x + 3) + (2x - 1) = 6x + 2 $$
For part ii:
$$ f + g = (2x^2) + (x + 1) = 2x^2 + x + 1 $$
- Calculate ( f - g )
For part i:
$$ f - g = (4x + 3) - (2x - 1) = 2x + 4 $$
For part ii:
$$ f - g = (2x^2) - (x + 1) = 2x^2 - x - 1 $$
- Calculate ( f \cdot g )
For part i:
$$ f \cdot g = (4x + 3)(2x - 1) = 8x^2 - 4x + 6x - 3 = 8x^2 + 2x - 3 $$
For part ii:
$$ f \cdot g = (2x^2)(x + 1) = 2x^3 + 2x^2 $$
- Calculate ( \frac{f}{g} )
For part i:
$$ \frac{f}{g} = \frac{4x + 3}{2x - 1} $$
For part ii:
$$ \frac{f}{g} = \frac{2x^2}{x + 1} $$
- Combine all expressions
For part i:
$$ (f + g)(f - g)(f \cdot g)(\frac{f}{g}) = (6x + 2)(2x + 4)(8x^2 + 2x - 3)\left(\frac{4x + 3}{2x - 1}\right) $$
For part ii:
$$ (f + g)(f - g)(f \cdot g)(\frac{f}{g}) = (2x^2 + x + 1)(2x^2 - x - 1)(2x^3 + 2x^2)\left(\frac{2x^2}{x + 1}\right) $$
- Final Expression
Calculate the final expressions for both parts accordingly.
For part i:
$$ (f + g)(f - g)(f \cdot g)(\frac{f}{g}) = (6x + 2)(2x + 4)(8x^2 + 2x - 3)\left(\frac{4x + 3}{2x - 1}\right) $$
For part ii:
$$ (f + g)(f - g)(f \cdot g)(\frac{f}{g}) = (2x^2 + x + 1)(2x^2 - x - 1)(2x^3 + 2x^2)\left(\frac{2x^2}{x + 1}\right) $$
More Information
The expressions derived in both parts involve a series of algebraic operations: addition, subtraction, multiplication, and division of polynomial functions. These kinds of problems illustrate the importance of algebra in manipulating functions.
Tips
- Forgetting to distribute correctly when multiplying expressions, leading to incorrect coefficients.
- Not simplifying fractions appropriately in ( \frac{f}{g} ).
- Ignoring the signs while performing the operations, particularly in subtraction.
AI-generated content may contain errors. Please verify critical information