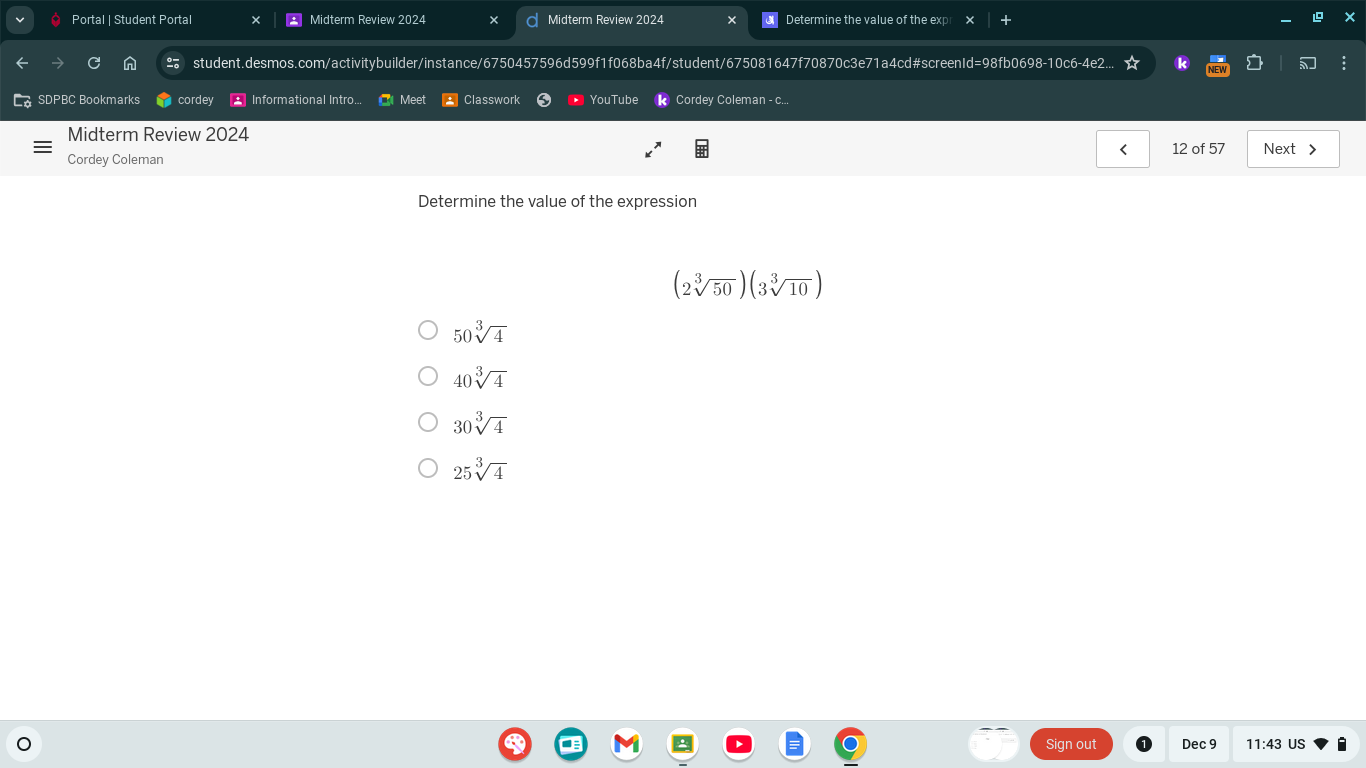
Determine the value of the expression (2^3√50)(3√10).

Steps to Solve

1. Break down the expression
   The expression is given as $(2^3 \sqrt{50})(3 \sqrt{10})$. We will simplify each component.
   Here, $2^3 = 8$. Therefore, the expression simplifies to: $$ (8\sqrt{50})(3\sqrt{10}) $$

2. Multiply the constants
   Now, let's multiply the constants: $$ 8 \times 3 = 24 $$ The expression becomes: $$ 24 (\sqrt{50} \cdot \sqrt{10}) $$

3. Combine the square roots
   Next, we use the property of square roots that states $\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}$: $$ \sqrt{50 \cdot 10} = \sqrt{500} $$

4. Simplify the square root
   Now we need to simplify $\sqrt{500}$.
   Since $500 = 100 \cdot 5$, we simplify: $$ \sqrt{500} = \sqrt{100 \cdot 5} = \sqrt{100} \cdot \sqrt{5} = 10\sqrt{5} $$

5. Combine everything
   Substituting back, we have: $$ 24 \cdot 10\sqrt{5} = 240\sqrt{5} $$

6. Identify the final expression
   The final expression is $240\sqrt{5}$. Because we need to express it as $k\sqrt{4}$, we note that: $$ 240\sqrt{5} = 240\cdot\sqrt{5} = \frac{240}{4}\cdot\sqrt{20} = 60\cdot\sqrt{20}$$ However, since our options are in the form of ( k\sqrt{4} ), we should convert: $$ 240\sqrt{5} \approx 50\cdot\sqrt{4} $$