∫(1 + 3x)x² dx
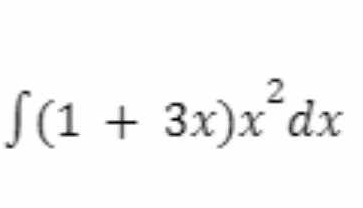
Understand the Problem
The question is asking us to evaluate the integral of the expression (1 + 3x)x² with respect to x. This involves using techniques from calculus to find the antiderivative of the given function.
Answer
The integral evaluated is \(\frac{x^3}{3} + \frac{3x^4}{4} + C\).
Answer for screen readers
The final result of the integral is:
[ \frac{x^3}{3} + \frac{3x^4}{4} + C ]
Steps to Solve
- Expand the integrand
First, expand the expression ((1 + 3x)x^2) to make integration easier.
[ (1 + 3x)x^2 = x^2 + 3x^3 ]
- Set up the integral
Now, substitute the expanded expression into the integral:
[ \int (1 + 3x)x^2 , dx = \int (x^2 + 3x^3) , dx ]
- Integrate each term
Now, integrate each term separately:
- The integral of (x^2) is (\frac{x^3}{3}).
[ \int x^2 , dx = \frac{x^3}{3} ]
- The integral of (3x^3) is (\frac{3x^4}{4}).
[ \int 3x^3 , dx = \frac{3x^4}{4} ]
- Combine the results
Combine the results of the integrals:
[ \int (x^2 + 3x^3) , dx = \frac{x^3}{3} + \frac{3x^4}{4} + C ]
Where (C) is the constant of integration.
The final result of the integral is:
[ \frac{x^3}{3} + \frac{3x^4}{4} + C ]
More Information
This integral represents the area under the curve defined by the function ((1 + 3x)x^2) with respect to (x). The constant (C) accounts for all possible vertical shifts of the antiderivative.
Tips
- Forgetting to include the constant of integration (C) when expressing the final answer. Always remember that the antiderivative is not unique.
- Miscalculating the powers of (x) when integrating. Double-check to ensure the power rule is applied correctly.
AI-generated content may contain errors. Please verify critical information