Solve the equation by graphing: 1/3 x + 5 = -2x - 2. x = ___
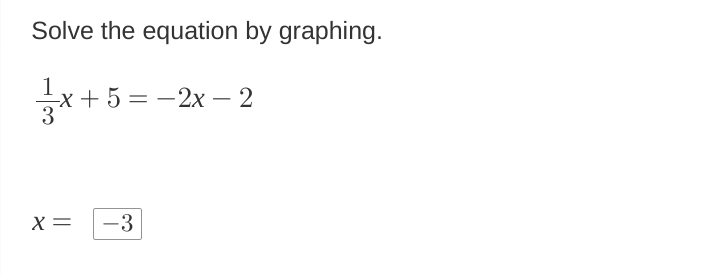
Understand the Problem
The question is asking us to solve the equation by graphing, which involves finding the value of x that satisfies the equation given. We need to represent the equation graphically and identify the point of intersection.
Answer
$x = -3$
Answer for screen readers
The solution to the equation is: $$ x = -3 $$
Steps to Solve
- Rearranging the equation
We start with the given equation: $$ \frac{1}{3}x + 5 = -2x - 2 $$
Next, rearrange this equation so we can graph both sides. Move all terms involving $x$ to one side and the constants to the other side:
$$ \frac{1}{3}x + 2x = -2 - 5 $$
- Combining like terms
Now, simplify the equation by combining like terms on each side. The left side will have $x$ terms, while the right side will simplify to a constant:
Combining like terms: $$ \frac{1}{3}x + 2x = \frac{1}{3}x + \frac{6}{3}x = \frac{7}{3}x $$
Now the equation looks like this: $$ \frac{7}{3}x = -7 $$
- Solving for x
To isolate $x$, multiply both sides by the reciprocal of $\frac{7}{3}$, which is $\frac{3}{7}$:
$$ x = -7 \cdot \frac{3}{7} $$
- Calculating the final value of x
Now perform the multiplication: $$ x = -3 $$
The solution to the equation is: $$ x = -3 $$
More Information
This method involves finding where two lines intersect, which is a graphical way to solve equations. The intersection point of the graphs of the two equations represents the solution.
Tips
- Forgetting to properly combine like terms.
- Misplacing signs when moving terms from one side to the other.
- Not using the correct reciprocal when isolating $x$.
AI-generated content may contain errors. Please verify critical information